Download Naskah Soal UN Matematika SMA IPS 2017 Asli

Hallo, Sobat Pejuang UN. Kali ini saya akan membagikan naskah soal UN Matematika SMA IPS tahun 2017. Berikut Soal-soalnya

Soal Nomor 1

Diketahui $x\neq 0$ dan $y\neq 0$ , bentuk sederhana dari $\left ( \dfrac{2x^{-5}y^{3}}{8x^{3}y^{-2}} \right )^2$ adalah.....
A. $\dfrac{y^{10}}{4x^{16}}$

B. $\dfrac{y^{2}}{4x^{4}}$

C. $\dfrac{y^{10}}{16x^{16}}$

D. $\dfrac{y^{2}}{16x^{4}}$

E. $\dfrac{16y^{10}}{x^{16}}$

Soal Nomor 2

Bentuk sederhana $\sqrt{75} + 2\sqrt{3} - \sqrt{12} + \sqrt{27}$ adalah.......
A. $2\sqrt{3}$
B. $5\sqrt{3}$
C. $8\sqrt{3}$
D. $12\sqrt{3}$
E. $34\sqrt{3}$

Soal Nomor 3

Nilai dari $^{7}log4.^{2}log5 + ^{7}log\dfrac{49}{25} =......$
A. 1
B. 2
C. 3
D. 4
E. 5

Soal Nomor 4

Diketahui fungsi $f\left ( x \right )=x^{2}+5x-15$ dan fungsi $g\left ( x \right )=x+2$. Fungsi komposisi $\left ( f\circ g \right )\left ( x \right )=......$
A. $x^{2} + 9x + 7$
B. $x^{2} + 9x - 1$
C. $x^{2} + 7x + 7$
D. $x^{2} + 5x + 7$
E. $x^{2} + 5x -1$

Soal Nomor 5

Fungsi $f: $  $R\rightarrow R$  didefinisikan $f\left ( x \right )=\dfrac{4x-7}{3-x},x\neq3$.
Invers dari $f(x)$ adalah $f^{-1}(x) = ........$

A. $\dfrac{3x-7}{x-4},x\neq4$.

B. $\dfrac{3x-7}{x+4},x\neq-4$.

C. $\dfrac{3x+3}{x-4},x\neq4$.

D. $\dfrac{3x+7}{x+4},x\neq-4$.

E. $\dfrac{3x+7}{x-4},x\neq4$.

Soal Nomor 6

Perhatikan gambar!

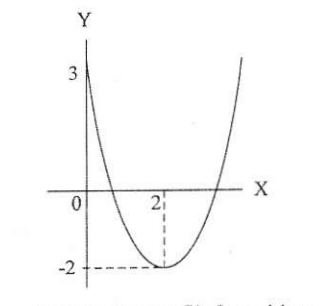
Persaman grafix fungsi kuadrat dari gambar tersebut adalah .......
A. $y=\dfrac{4}{5}x^{2}-4x + 3$

B. $y=\dfrac{5}{4}x^{2}-5x + 3$

C. $y=\dfrac{4}{5}x^{2}+4x - 3$

D. $y=\dfrac{5}{4}x^{2}-5x - 3$

F. $y=\dfrac{5}{4}x^{2}+5x + 3$

Soal Nomor 7

Misalkan $x_{1}$ dan $x_{2}$ adalah akar-akar persamaan kuadrat $x^{2}+3x-28=0$. Jika $x_{1} < x_{2},$ maka nilai $3x_{1}+2x_{2}$ adalah ......
A. $-13$
B. $-3$
C. $-2$
D. $2$
E. $13$

Soal Nomor 8

Misalkan $x_{1}$ dan $x_{2}$ adalah akar-akar persamaan kuadrat $2x^{2}+6x+7=0$. Persamaan kuadrat yang akar-akarnya $\left ( 2x_{1}+1 \right )$ dan $\left ( 2x_{2}+1 \right )$ adalah ........
A. $x^{2}-8x+9=0$
B. $x^{2}-8x+14=0$
C. $x^{2}-8x+21=0$
D. $x^{2}-4x+9=0$
E. $x^{2}-4x+21=0$

Soal Nomor 9

Total penjualan suatu barang $\left ( k\right )$ merupakan perkalian antara harga $\left ( p\right )$ dan permintaan $\left ( x\right )$ dinyatakan dengan $k = px$. Untuk $p=90-3x$ dalam jutaan rupiah dan $1\leq x\leq 30$, maka total penjualan maksimum adalah .........
A. Rp. 1.350.000.000,00
B. Rp. 675.000.000,00
C. Rp. 600.000.000,00
D. Rp. 450.000.000,00
E. Rp. 45.000.000,00

Soal Nomor 10

Misalkan $\left ( a,b\right )=\left ( a_{1},b_{1}\right )$ adalah penyelesaian dari sistem persamaan $\left\{\begin{matrix} 2a-7b=-16 & \\ a+8b=15& \end{matrix}\right.,$ maka nilai $a_{1}+2b_{1}$ adalah ........

A. $-3$
B. $-1$
C. $0$
D. $1$
E. $3$

Soal Nomor 11

Daerah yang diarsir pada grafix di bawah ini merupakan penyelesaian dari sistem pertidaksamaan .............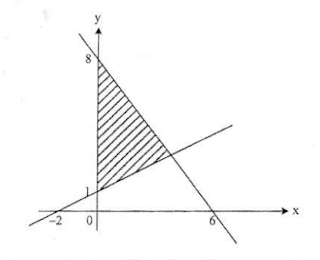


A. $2x-y\leq2,$   $4x+3y\leq24,$   $x\geq0,y\geq0$
B. $2y-x\leq2,$   $4x+3y\geq24,$   $x\geq0,y\geq0$
C. $2y-x\leq2,$   $4x+3y\leq24,$   $x\geq0,y\geq0$
D. $2y-x\geq2,$   $4x+3y\leq24,$   $x\geq0,y\geq0$
E. $2x-y\geq2,$   $4x+3y\leq24,$   $x\geq0,y\geq0$

Soal Nomor 12

Seorang peternak memiliki tidak lebih dari 8 kandang untuk memelihara kambing dan sapi. Setiap kandang dapat menampung kambing sebanyak 15 ekor atau menampung sapi sebanyak 6 ekor. Jumlah ternak yang direncanakan tidak lebih dari 100 ekor. Jika banyak kandang yang berisi kambing $x$ buah dan yang berisi sapi $y$ buah, model matematika untuk kegiatan peternak tersebut adalah .......
A. $8x + 6y\leq 100,$     $x + y \leq 8$,    $x\geq0,y\geq0$
B. $15x + 6y\leq 100,$     $x + y \leq 8$,    $x\geq0,y\geq0$
C. $6x + 15y\leq 100,$     $x + y \leq 8$,    $x\geq0,y\geq0$
D. $6x + 8y\leq 100,$     $x + y \leq 8$,    $x\geq0,y\geq0$
E. $15x + 8y\leq 100,$     $x + y \leq 8$,    $x\geq0,y\geq0$

Soal Nomor 13

Diketahui sistem pertidaksamaan $5x + 2y \leq 80,$ $x + 4y \geq 25,$ $x\geq0, y\geq0.$ Nilai maksimum dari $f\left ( x,y \right )=100x + 4y$ yang memenuhi pertidaksamaan tersebut adalah .......
A. 25
B. 160
C. 1510
D. 1600
E. 2500

Soal Nomor 14

Sebuah toko kain menyediakan dua jenis kain batik yaitu batik halus dan batik cap. Etalase kain batik toko tersebut dapat menampung maksimum sebanyak 36 kain batik. Harga satuan kain batik halus Rp. 800.000,00 dan harga satuan kain batik cap Rp. 600.000,00. Modal yang disediakan untuk penyediaan kain batik tidak lebih dari Rp. 24.000.000,00. Keuntungan penjualan adalah Rp. 120.000,00 per kain batik halus dan Rp. 100.000,00 per kain batik cap. Banyak kain batik yang harus disediakan agar diperoleh keuntungan maksimum dari penjualan semua kain batik tersebut adalah .......
A. 36 kain batik halus saja
B. 36 kain batik halus dan 30 kain batik cap
C. 30 kain batik halus dan 36 kain batik cap
D. 24 kain batik halus dan 12 kain batik cap
E. 12 kain batik halus dan 24 kain batik cap

Soal Nomor 15

Ibu Giat dan Ibu Pretasi berbelanja di toko Bahagia. Ibu Giat membeli 2 kg gula dan 3 kg beras, dan ia harus membayar Rp. 64.000,00. Sedangkan Ibu Prestasi membeli 5 kg gula dan 4 kg beras, dan ia harus membayar Rp. 118.000,00. Toko Bahagia menjual gula dengan harga $x$ rupiah tiap kilo dan beras dengan harga $y$ rupiah tiap kilo. Permasalahan tersebut dapat ditampilkan dalam bentuk persamaan matriks......
$A. \begin{pmatrix} 2 & 3\\ 5 & 4 \end{pmatrix} \begin{pmatrix} x & y \end{pmatrix} = \begin{pmatrix} 64.000 \\ 118.000 \end{pmatrix}$

$B. \begin{pmatrix} 2 & 3\\ 5 & 4 \end{pmatrix} \begin{pmatrix} x & y \end{pmatrix} = \begin{pmatrix} 64.000 & 118.000 \end{pmatrix}$

$C. \begin{pmatrix} 2 & 3\\ 5 & 4 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 64.000 \\ 118.000 \end{pmatrix}$

$D. \begin{pmatrix} 2 & 5\\ 3 & 4 \end{pmatrix} \begin{pmatrix} x & y \end{pmatrix} = \begin{pmatrix} 64.000 & 118.000 \end{pmatrix}$

$E. \begin{pmatrix} 2 & 5\\ 3 & 4 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 64.000 \\ 118.000 \end{pmatrix}$

Soal Nomor 16

Diketahui matriks $A= \begin{pmatrix} 2 & a\\ b & 1 \end{pmatrix}, $ $B= \begin{pmatrix} 1 & 4\\ b+1 & c \end{pmatrix} ,$ dan $C= \begin{pmatrix} 3 & 5\\ 0 & 4 \end{pmatrix} .$    Jika $A + B = C^{T}$ dengan $C^{T}$ menyatakan transpose matriks $C,$ maka nilai $a -2b + c$ adalah ......
A. $-8$
B. $-5$
C. $-2$
D.  $0$
E.  $5$

Soal Nomor 17

Diketahui matriks $A= \begin{pmatrix} 3 & -2\\ 5 & 5 \end{pmatrix}$ dan matriks $B= \begin{pmatrix} 1 & 5\\ 4 & 3 \end{pmatrix}.$ Determinan $A$X$B$ adalah .......
A. $-391$
B. $-119$
C. $-41$
D. $41$
E. $391$

Soal Nomor 18

Diketahui barisan aritmetika dengan suku ke -5 dan suku ke-8 berturut-turut adalah 4 dan 10. Jumlah sepuluh suku pertama deret tersebut adalah ......
A. 50
B. 55
C. 60
D. 65
E. 70

Soal Nomor 19

Diketahui suku ke -2 dan ke -6 barisan geometri berturut-turut adalah 4 dan 64 . Suku ke -10 barisan tersebut adalah ......
A. 1.024
B. 512
C. 256
D. 128
E. 64

Soal Nomor 20

Pertumbuhan penduduk suatu kota setiap tahun diasumsikan mengikuti aturan barisan geometri. Pada tahun 2013 pertambahannya sebanyak 5 orang dan pada tahun 2015 sebanyak 80 orang. Pertambahan penduduk pada tahun 2017 adalah .........
A. 256 orang
B. 512 orang
C. 1.280 orang
D. 2.560 orang
E. 5.024 orang

Soal Nomor 21

Suatu perusahaan pada tahun pertama memproduksi 9.000 unit barang. Pada tahun-tahun berikutnya produksi turun secara tetap sebesar 10% dari tahun sebelumnya. Perusahaan tersebut akan memproduksi barang tersebut pada tahun ketiga sebanyak ..........
A. 4.930 unit
B. 5.780 unit
C. 6.561 unit
D. 7.290 unit
E. 8.100 unit

Soal Nomor 22

Nilai $\lim_{x\rightarrow 2}\dfrac{2x^{2} + 2x -12}{x^{2} -6x + 8} = .......$

A. $-5$
B. $-2$
C. $0$
D. $2$
E. $5$

Soal Nomor 23

Nilai $\lim_{x\rightarrow \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )} adalah= .......$

A. $-4$
B. $-2$
C. $2$
D. $4$
E. $8$

Soal Nomor 24

Jika $f'\left ( x \right )$ turunan pertama dari $f\left ( x \right )=x^{3} -9x + 5,$ maka nilai $f'\left ( 1 \right )$ adalah .......
A. $-12$
B. $-6$
C. $0$
D. $6$
E. $12$

Soal Nomor 25

Grafik fungsi $f\left ( x \right )=2x^{3} - 3x^{2} -72x -9,$ naik pada interval ........
$A.x < -3$ atau $x > 4$
$B. x < -4$ atau $x > 3$
$C. x < 1$ atau $x > 4$
$D. -3 < x < 4$
$E. -4 < x < 3$

Soal Nomor 26

Hasil dari $\int\left ( 10x^{4}- 6x^{2} -4x \right )dx$ adalah ......
A.$40x^{3} - 12x - 4 + C$
B. $5x^{5} - 3x^{3} - 2x^{2} + C$
C. $2x^{5} - 2x^{3} - 2x^{2} + C$
D. $2x^{5} + 3x^{3} - 2x^{2} + C$
E. $2x^{5} - 3x^{3} - 4x^{2} + C$

Soal Nomor 27

Hasil dari $\int_{-1}^{3}\left ( 6x^{2} + 5\right )dx$ adalah ........
A. $103$
B. $76$
C. $62$
D. $40$
E. $26$

Soal Nomor 28

Diketahui kubus ABCD.EFGH seperti pada gambar berikut. Jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis ........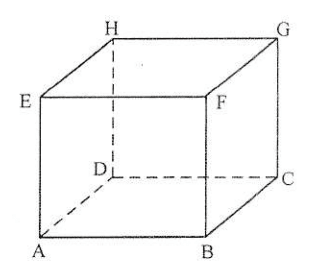

A. AC
B. AD
C. AH
D. AF
E. AG

Soal Nomor 29

Diketahui limas beraturan T. ABCD dengan rusuk alas $6$ cm dan rusuk tegak $6\sqrt{2} $ cm. Jika antara garis OT dan AT membentuk sudut $\lambda $. besar sudut $\lambda $ adalah .......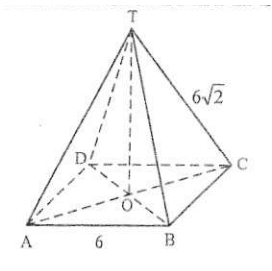

A. $0^{\circ}$
B. $30^{\circ}$
C. $45^{\circ}$
D. $60^{\circ}$
E. $90^{\circ}$

Soal Nomor 30

Diketahui $\Delta $KLM siku-siku di M dan tan $L=\dfrac{1}{3}\sqrt{3}.$  Nilai cos $L$ adalah .....
A. $\dfrac{1}{2}\sqrt{2}$

B. $\dfrac{1}{2}\sqrt{3}$

C. $\dfrac{1}{2}$

D. $\sqrt{2}$
E. $\sqrt{3}$

Soal Nomor 31

Himpunan penyelesaian dari persamaan $1 + 2 sinx = 0,$ untuk $0^{\circ}\leq x \leq 360^{\circ}$ adalah .......
A. $\left\{ 120^{\circ}, 180^{\circ}\right\}$
B. $\left\{ 150^{\circ}, 260^{\circ}\right\}$
C. $\left\{ 180^{\circ}, 270^{\circ}\right\}$
D. $\left\{ 200^{\circ}, 320^{\circ}\right\}$
E. $\left\{ 210^{\circ}, 330^{\circ}\right\}$

Soal Nomor 32

Diketahui sudut elevansi pengamat terhadap puncak suatu menara televisi adalah $60^{\circ}$ dan jarak pengamat dari kaki menara 400 m. Tinggi menara tersebut adalah ........
A. $800 $ m
B. $400\sqrt{3}$ m
C. $400\sqrt{2}$ m
D. $\dfrac{400}{3}\sqrt{2}$ m
E. $200$ m

Soal Nomor 33

Tabel berikut adalah nilai hasil tes siswa yang di terima di kelas $X $ IPA.

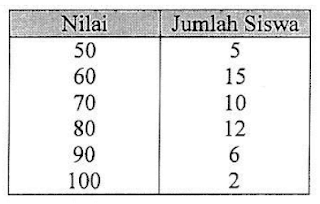
Siswa yang lulus dan dapat di terima adalah mereka yang mendapat nilai minimal 70. Persentase siswa yang tidak diterima adalah ......
A. 20%
B. 35%
C. 40%
D. 50%
E. 60%

Soal Nomor 34

Nilai yang diperoleh peserta lomba matematika SMA tahun 2016 disajikan dalam histogram berikut.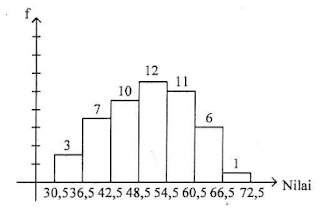

Median dari nilai lomba matematika tersebut adalah ........
A.  51,0
B.  51,5
C.  52,0
D.  52,5
E.  53,0

Soal Nomor 35

Varian dari data 2, 5, 7, 6, 4, 5, 8, 3 adalah .......
A. $0$

B. $\dfrac{12}{8}$

C.$\dfrac{14}{8}$

D.$\dfrac{18}{8}$

E.$\dfrac{28}{8}$

Soal Nomor 36

Dari angka-angka 0, 1, 3, 6, 7, 9 akan dibentuk bilangan genap yang terdiri atas tiga angka berlainan. Banyak bilangan yang mungkin dapat dibentuk adalah .........
A. 20
B. 24
C. 32
D. 36
E. 48

Soal Nomor 37

Panitia lomba yang terdiri atas ketua, wakil ketua, sekretaris, bendahara, dan humas akan dipilih dari 2 orang pria dan 3 orang wanita. Jika posisi ketua dan humas harus diisi pria, pilihan susunan panitia yang dapat dibentuk sebanyak .........
A. 6
B. 8
C. 10
D. 12
E. 120

Soal Nomor 38

Banyak cara membentuk grup musik yang terdiri atas 4 musisi yang dipilih dari 7 musisi adalah .......
A. 35
B. 70
C. 210
D. 560
E. 840

Soal Nomor 39

Peluang munculnya mata dadu ganjil atau kelipatan 3 pada pelemparan sebuah dadu adalah ........
A. $\dfrac{5}{6}$

B. $\dfrac{1}{2}$

C. $\dfrac{2}{3}$

D. $\dfrac{1}{4}$

E. $\dfrac{1}{6}$

Soal Nomor 40

Tiga uang keping logam dilempar undi bersama-sama sebanyak 40 kali. Frekuensi harapan muncul 2 angka dan 1 gambar adalah ........
A. 5
B. 10
C. 15
D. 30
E. 35


Terima Kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel singkat ini yang berjudul "Download Naskah Soal UN Matematika SMA IPS 2017 Asli". Semoga informasi yang terkandung dalam artikel ini dapat bermanfaat bagi anda yang membutuhkannya.


Salam sukses untuk kita semua.