Pembahasan Soal UN Matematika SMA IPS No. 21 - 25_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMA IPS tahun 2017 part 5. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Aplikasi Barisan Geometri dalam kehidupan sehari-hari (soal cerita)
- Limit Fungsi Aljabar
- Limit Mendekati Tak Hingga
- Turunan Fungsi Aljabar
- Kemonotonan dan Kecekungan Kurva_BAB Turunan
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMA IPS 2017 Part.1 No. 1 - 5
2. Pembahasan Soal UN Matematika SMA IPS 2017 Part.2 No. 6 - 10
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.3 No. 11-15
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.4 No. 16-20
Soal Nomor 21
Suatu perusahaan pada tahun pertama memproduksi 9.000 unit barang. Pada tahun-tahun berikutnya produksi turun secara tetap sebesar 10% dari tahun sebelumnya. Perusahaan tersebut akan memproduksi barang tersebut pada tahun ketiga sebanyak ..........A. 4.930 unit
B. 5.780 unit
C. 6.561 unit
D. 7.290 unit
E. 8.100 unit
Pembahasan Soal Nomor 21
Diketahui :
Produksi tahun pertama = 9.000 unit barang
Produksi tahun berikutnya turun 10% dari tahun sebelumnya = Hal ini berarti bahwa produksi tahun berikutnya hanya sebanyak 90% saja dari tahun sebelumnya.
Ditanyakan produksi barang tahun ketiga ???
Penyelesaian :
Cara I (Manual)
Tahun I $= 9.000$ unit
Tahun II $= 90\% \times 9.000 = 8.100$ unit
Tahun III $= 90\% \times 8.100 = 7.290$ unit
Cara II (Menggunakan Rumus Barisan Geometri)
$a = 9.000$
$r = 100\% - 10\%$
$r = 90\%$
$r = 0,9$
Maka produksi barang tahun ke 3 adalah ...
$U_{n} = ar^{n-1}$
$U_{3} = ar^{2}$
$U_{3} = 9000 \times 0,9^{2}$
$U_{3} = 9000 \times 0,81$
$U_{3} = 7290$
Jadi, Perusahaan tersebut akan memproduksi barang tersebut pada tahun ketiga sebanyak 7290
Jawab : D
Produksi tahun pertama = 9.000 unit barang
Produksi tahun berikutnya turun 10% dari tahun sebelumnya = Hal ini berarti bahwa produksi tahun berikutnya hanya sebanyak 90% saja dari tahun sebelumnya.
Ditanyakan produksi barang tahun ketiga ???
Penyelesaian :
Cara I (Manual)
Tahun I $= 9.000$ unit
Tahun II $= 90\% \times 9.000 = 8.100$ unit
Tahun III $= 90\% \times 8.100 = 7.290$ unit
Cara II (Menggunakan Rumus Barisan Geometri)
$a = 9.000$
$r = 100\% - 10\%$
$r = 90\%$
$r = 0,9$
Maka produksi barang tahun ke 3 adalah ...
$U_{n} = ar^{n-1}$
$U_{3} = ar^{2}$
$U_{3} = 9000 \times 0,9^{2}$
$U_{3} = 9000 \times 0,81$
$U_{3} = 7290$
Jadi, Perusahaan tersebut akan memproduksi barang tersebut pada tahun ketiga sebanyak 7290
Jawab : D
Soal Nomor 22
Nilai $\displaystyle \lim_{x\to 2}\dfrac{2x^{2} + 2x -12}{x^{2} -6x + 8} = .......$
A. $-5$
B. $-2$
C. $0$
D. $2$
E. $5$
Pembahasan Soal Nomor 22
Rumus-rumus yang digunakan :
Untuk menyelesaikan soal limit di atas, ada dua cara yang bisa digunakan yaitu : Pertama dengan Cara Memfaktorkan dan Kedua dengan menggunakan turunan atau dalil L'Hospital
Cara I (Memfaktorkan)
$\begin{align} \displaystyle \lim_{x \to 2} \frac{2x^{2}+2x-12}{x^{2}-6x+8} & = \displaystyle \lim_{x \to 2 } \frac{2 \left (x^{2}+x-6 \right)}{x^{2}-6x+8} \\ & = \displaystyle \lim_{x \to 2 } \frac{2 \left (x+3 \right) \left (x-2 \right)}{\left (x-4 \right) \left (x-2 \right)} \\ & = \displaystyle \lim_{x \to 2} \frac{2 \left ( x + 3 \right) }{\left (x-4 \right)} \\ & = \frac{ 2 \left ( 2 + 3 \right) }{\left ( 2 - 4 \right) } \\ & = \frac{ 10 }{-2} \\ & = -5 \end{align}$
Cara II (Turunan / dalil L'Hospital)
$\begin{align} \displaystyle \lim_{x \to 2 } \frac{ 2x^{2} + 2x -12 }{x^{2} -6x + 8} & = \displaystyle \lim_{x \to 2 } \frac{ 4x + 2}{ 2x - 6} \\ & = \frac{ 4 \left ( 2 \right) + 2 }{ 2 \left ( 2 \right) - 6} \\ & = \frac{ 10 }{-2} \\ & = -5 \end{align}$
Jawab : A
Untuk menyelesaikan soal limit di atas, ada dua cara yang bisa digunakan yaitu : Pertama dengan Cara Memfaktorkan dan Kedua dengan menggunakan turunan atau dalil L'Hospital
Cara I (Memfaktorkan)
$\begin{align} \displaystyle \lim_{x \to 2} \frac{2x^{2}+2x-12}{x^{2}-6x+8} & = \displaystyle \lim_{x \to 2 } \frac{2 \left (x^{2}+x-6 \right)}{x^{2}-6x+8} \\ & = \displaystyle \lim_{x \to 2 } \frac{2 \left (x+3 \right) \left (x-2 \right)}{\left (x-4 \right) \left (x-2 \right)} \\ & = \displaystyle \lim_{x \to 2} \frac{2 \left ( x + 3 \right) }{\left (x-4 \right)} \\ & = \frac{ 2 \left ( 2 + 3 \right) }{\left ( 2 - 4 \right) } \\ & = \frac{ 10 }{-2} \\ & = -5 \end{align}$
Cara II (Turunan / dalil L'Hospital)
$\begin{align} \displaystyle \lim_{x \to 2 } \frac{ 2x^{2} + 2x -12 }{x^{2} -6x + 8} & = \displaystyle \lim_{x \to 2 } \frac{ 4x + 2}{ 2x - 6} \\ & = \frac{ 4 \left ( 2 \right) + 2 }{ 2 \left ( 2 \right) - 6} \\ & = \frac{ 10 }{-2} \\ & = -5 \end{align}$
Jawab : A
Soal Nomor 23
Nilai $\displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )}$ adalah = .......A. $-4$
B. $-2$
C. $2$
D. $4$
E. $8$
Pembahasan Soal Nomor 23
Rumus-rumus yang digunakan :
Rumus Alternatif Limit x Mendekati Tak hingga
Untuk menyelesaikan soal Limit X mendekati Tak hingga adalah dengan cara membagi dengan pangkat tertinggi.
Namun apabila anda ingin menggunakan cara yang lebih cepat, anda bisa menggunakan Rumus Alternatif yang sudah saya tulis di atas.
Cara 1 (Cara Cepat)
$\begin{align} \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )} & = \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2} {4x^{2} - 4x - 3} \\ & = \dfrac {8}{4} \\ & = 2 \end{align}$
Perhatikan pangkat tertinggi pada limit fungsi di atas!
Pangkat tertinggi pada pembilang dan pangkat tertinggi pada penyebut sama tinggi atau sama besar
Karena pembilang dan penyebut mempunyai pangkat tertinggi sama, maka nilai limitnya merupakan koefisien dari pangkat tertinggi tersebut. (lihat rumusnya biar lebih joss, #syarat no. 2)
Cara Biasa (Membagi dengan pangkat tertinggi)
$\begin{align} \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )} & = \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2} {4x^{2} - 4x - 3} \\ & = \displaystyle \lim_{x \to \infty}\dfrac{\dfrac {8x^{2}}{x^{2}} - \dfrac {5x}{x^{2}} + \dfrac{2}{x^{2}}} {\dfrac {4x^{2}}{x^{2}} - \dfrac {4x}{x^{2}} - \dfrac{3}{x^{2}}} \\ & = \displaystyle \lim_{x \to \infty}\dfrac{8 - \dfrac {5}{x} + \dfrac{2}{x^{2}}} {4x - \dfrac {4}{x} - \dfrac{3}{x^{2}}} \\ & = \dfrac {8-0+0}{4-0-0} \\ & = \dfrac {8}{4} \\ & = 2 \end{align}$
Jawab : C
Rumus Alternatif Limit x Mendekati Tak hingga
Untuk menyelesaikan soal Limit X mendekati Tak hingga adalah dengan cara membagi dengan pangkat tertinggi.
Namun apabila anda ingin menggunakan cara yang lebih cepat, anda bisa menggunakan Rumus Alternatif yang sudah saya tulis di atas.
Cara 1 (Cara Cepat)
$\begin{align} \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )} & = \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2} {4x^{2} - 4x - 3} \\ & = \dfrac {8}{4} \\ & = 2 \end{align}$
Perhatikan pangkat tertinggi pada limit fungsi di atas!
Pangkat tertinggi pada pembilang dan pangkat tertinggi pada penyebut sama tinggi atau sama besar
Karena pembilang dan penyebut mempunyai pangkat tertinggi sama, maka nilai limitnya merupakan koefisien dari pangkat tertinggi tersebut. (lihat rumusnya biar lebih joss, #syarat no. 2)
Cara Biasa (Membagi dengan pangkat tertinggi)
$\begin{align} \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2}{\left ( 2x-3 \right )\left ( 2x+1 \right )} & = \displaystyle \lim_{x \to \infty}\dfrac{8x^{2} - 5x + 2} {4x^{2} - 4x - 3} \\ & = \displaystyle \lim_{x \to \infty}\dfrac{\dfrac {8x^{2}}{x^{2}} - \dfrac {5x}{x^{2}} + \dfrac{2}{x^{2}}} {\dfrac {4x^{2}}{x^{2}} - \dfrac {4x}{x^{2}} - \dfrac{3}{x^{2}}} \\ & = \displaystyle \lim_{x \to \infty}\dfrac{8 - \dfrac {5}{x} + \dfrac{2}{x^{2}}} {4x - \dfrac {4}{x} - \dfrac{3}{x^{2}}} \\ & = \dfrac {8-0+0}{4-0-0} \\ & = \dfrac {8}{4} \\ & = 2 \end{align}$
Jawab : C
Soal Nomor 24
Jika $f'\left ( x \right )$ turunan pertama dari $f\left ( x \right )=x^{3} -9x + 5,$ maka nilai $f'\left ( 1 \right )$ adalah .......A. $-12$
B. $-6$
C. $0$
D. $6$
E. $12$
Pembahasan Soal Nomor 24
Rumus Turunan Fungsi Aljabar
Sekarang mari kita cari turunan fungsi aljabar dengan menggunakan rumus di atas. Lalu, setelah itu kita subtitusikan nilai $x=1$
$f\left ( x \right )=x^{3} -9x + 5$
$f^{'}\left(x\right)=3x^{2}-9$
$\begin{align} f'\left ( 1 \right ) & = 3x^{2}-9\\ & = 3\left(1\right)^{2} -9 \\ & = 3-9\\ & = -6 \end{align}$
Jadi, nilai $f'\left ( 1 \right )$ adalah $-6$
Jawab : B
$f\left (x\right)=ax^{n}\rightarrow$ maka $f^{'}\left(x\right)=anx^{n-1}$
Dengan a dan n bilangan real
Dengan a dan n bilangan real
Sekarang mari kita cari turunan fungsi aljabar dengan menggunakan rumus di atas. Lalu, setelah itu kita subtitusikan nilai $x=1$
$f\left ( x \right )=x^{3} -9x + 5$
$f^{'}\left(x\right)=3x^{2}-9$
$\begin{align} f'\left ( 1 \right ) & = 3x^{2}-9\\ & = 3\left(1\right)^{2} -9 \\ & = 3-9\\ & = -6 \end{align}$
Jadi, nilai $f'\left ( 1 \right )$ adalah $-6$
Jawab : B
Soal Nomor 25
Grafik fungsi $f\left ( x \right )=2x^{3} - 3x^{2} -72x -9,$ naik pada interval ........$A.x < -3$ atau $x > 4$
$B. x < -4$ atau $x > 3$
$C. x < 1$ atau $x > 4$
$D. -3 < x < 4$
$E. -4 < x < 3$
Pembahasan Soal Nomor 25
Fungsi naik atau turun disebut fungsi monoton.
Interval fungsi monoton dapat di nyatakan sebagai berikut :
1. fungsi f(x) naik jika f'(x) > 0
2. fungsi f(x) turun jika f'(x) < 0
Penyelesaian :
$f\left ( x \right )=2x^{3} - 3x^{2} -72x -9$
$f^{'}\left ( x \right )=6x^{2} - 6x -72$
Grafik fungsi f(x) naik jika f'(x) > 0
$f^{'}\left ( x \right )>0$
$6x^{2} - 6x -72>0$
$x^{2} - x -12>0$
$\left(x - 4\right)\left(x + 3\right)>0$
$x = 4$ atau $x = -3$
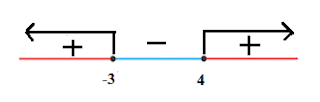
Selanjutnya kita buat garis bilangan untuk pertidaksamaan di atas.
Karena tanda pertidaksamaannya $" > "$ interval daerah pertidaksamaannya berada di sebelah kiri $−3$ atau sebelah kanan $4$.
Jadi, grafik fungsi $f(x)$ naik pada interval $x < −3$ atau $x > 4$
Jawab : A
Interval fungsi monoton dapat di nyatakan sebagai berikut :
1. fungsi f(x) naik jika f'(x) > 0
2. fungsi f(x) turun jika f'(x) < 0
Penyelesaian :
$f\left ( x \right )=2x^{3} - 3x^{2} -72x -9$
$f^{'}\left ( x \right )=6x^{2} - 6x -72$
Grafik fungsi f(x) naik jika f'(x) > 0
$f^{'}\left ( x \right )>0$
$6x^{2} - 6x -72>0$
$x^{2} - x -12>0$
$\left(x - 4\right)\left(x + 3\right)>0$
$x = 4$ atau $x = -3$
Selanjutnya kita buat garis bilangan untuk pertidaksamaan di atas.
Karena tanda pertidaksamaannya $" > "$ interval daerah pertidaksamaannya berada di sebelah kiri $−3$ atau sebelah kanan $4$.
Jadi, grafik fungsi $f(x)$ naik pada interval $x < −3$ atau $x > 4$
Jawab : A
Demikianlah pembahasan soal UN Matematika SMA IPS 2017 part.5 No. 21 -25 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
Pembahasan Soal UN Matematika SMA IPS 2017 Part.6 No. 26 - 30
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMA IPS No. 21 - 25". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini

PERHATIAN !!!
Terima Kasih Telah Berkunjung ke Blog Caraono.com
1. Berkomentarlah dengan Baik dan Sopan
2. No Link Aktif
3. Mohon Maaf apabila ada pertanyaan anda yang belum atau tidak bisa dijawab karena saya manusia biasa bukan Google
Thanks for visiting and the comment :)
EmoticonEmoticon