Pembahasan Soal UN Matematika SMA IPS 2017 No. 26 - 30

Pembahasan Soal UN Matematika SMA IPS No. 26 - 30_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMA IPS tahun 2017 part 6. Pada edisi kali ini soal-soalnya berisikan materi tentang :

1. Integral Tak Tentu Fungsi Aljabar
2. Integral Tentu Fungsi Aljabar
3. Jarak Titik ke Bidang Ruang Dimensi Tiga
4. Turunan Fungsi Aljabar
5. Mencari Nilai Cos Segitiga_Trigonometri

Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMA IPS 2017 Part.1 No. 1 - 5
2. Pembahasan Soal UN Matematika SMA IPS 2017 Part.2 No. 6 - 10
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.3 No. 11-15
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.4 No. 16-20
4. Pembahasan Soal UN Matematika SMA IPS 2017 Part.5 No. 21-25

Soal Nomor 26

Hasil dari $\int\left ( 10x^{4}- 6x^{2} -4x \right )dx$ adalah ......
A.$40x^{3} - 12x - 4 + C$
B. $5x^{5} - 3x^{3} - 2x^{2} + C$
C. $2x^{5} - 2x^{3} - 2x^{2} + C$
D. $2x^{5} + 3x^{3} - 2x^{2} + C$
E. $2x^{5} - 3x^{3} - 4x^{2} + C$

Pembahasan Soal Nomor 26

Rumus-rumus yang digunakan :
Rumus Integral tak tentu

$1. \int x^{n} dx = \dfrac {1}{n+1} x^{n+1} + C $

$2. \int kx^{n} dx = \dfrac {k}{n+1} x^{n+1} + C $

dimana $n \neq -1$

Penyelesaian :
$\int\left ( 10x^{4}- 6x^{2} -4x \right )dx \\ = \dfrac{10}{4+1}x^{4+1}- \dfrac{6}{2+1}x^{2+1} -\dfrac{4}{1+1}x^{1+1} + C \\ = \dfrac{10}{5}x^{5}- \dfrac{6}{3}x^{3} -\dfrac{4}{2}x^{2} + C \\ = 2x^{5}- 2x^{3} -2x^{2} + C $


Jawab : C

Soal Nomor 27

Hasil dari $\int_{-1}^{3}\left ( 6x^{2} + 5\right )dx$ adalah ........
A. $103$
B. $76$
C. $62$
D. $40$
E. $26$

Pembahasan Soal Nomor 27

Rumus-rumus yang digunakan :
Teorema Integral Tentu

$\begin{align} \int_{a}^{b}f \left (x\right) dx & = [F(x)]_{a}^{b} \\ & = F\left(b\right) - F\left(a\right)\\ \end{align}$

Penyelesaian :
$ \int_{-1}^{3}\left ( 6x^{2} + 5\right )dx\\ = 2x^{3} + 5x]_{-1}^{3} \\ = \left [2\left(3^{3}\right) + 5\left(3\right)\right] - \left [2\left(-1^{3}\right) + 5\left(-1\right)\right]\\ = \left (54 + 15\right) -\left (-2-5\right)\\ = 69 + 7\\ = 76$


Jawab : B

Soal Nomor 28

Diketahui kubus ABCD.EFGH seperti pada gambar berikut. Jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis ........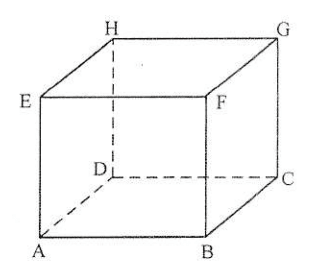

A. AC
B. AD
C. AH
D. AF
E. AG

Pembahasan Soal Nomor 28

Berdasarkan gambar di atas,
Jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis...(AD)


Jawab : B

Soal Nomor 29

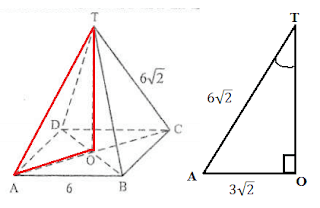
Diketahui limas beraturan T. ABCD dengan rusuk alas $6$ cm dan rusuk tegak $6\sqrt{2} $ cm. Jika antara garis OT dan AT membentuk sudut $\lambda $. besar sudut $\lambda $ adalah .......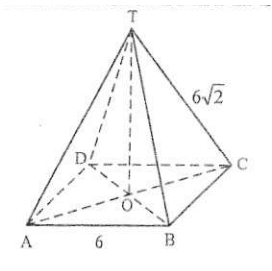

A. $0^{\circ}$
B. $30^{\circ}$
C. $45^{\circ}$
D. $60^{\circ}$
E. $90^{\circ}$

Pembahasan Soal Nomor 29

Penyelesaian :
$AT = CT = 6\sqrt {2}$
$AB = r = 6 cm$
$AC = r \sqrt{2}$
AO adalah setengah panjang diagonal AC
$AO=\dfrac {1}{2}AC\rightarrow$ maka $AO = \dfrac {1}{2}r \sqrt{2}$

maka panjang AO adalah ....
$\begin{align} AO & = \dfrac {1}{2}r \sqrt{2}\\ & = \dfrac {1}{2}\times 6 \times \sqrt{2}\\ & = 3 \sqrt{2} \end{align} $


Perhatikan gambar segitiga $AOT$ di atas !!!
Panjang Sisi $AO$ dan panjang sisi $AT$ sudah di ketahui, maka untuk mencari besar sudut alfa $\lambda $ dapat menggunakan sinus.

Rumus Sinus = ‘demi’ (sisi depan sudut dibagi sisi miring)

$\begin{align} \sin \alpha & = \dfrac {AO}{AT}\\ & = \dfrac {3\sqrt{2}}{6\sqrt{2}} \\ & = \dfrac {1}{2}\\ & = 30^{\circ} \end{align}$

Jadi, besar sudut antara garis OT dan AT adalah $30^{\circ}$
Jawab : B

Soal Nomor 30

Diketahui $\Delta $KLM siku-siku di M dan tan $L=\dfrac{1}{3}\sqrt{3}.$  Nilai cos $L$ adalah .....
A. $\dfrac{1}{2}\sqrt{2}$

B. $\dfrac{1}{2}\sqrt{3}$

C. $\dfrac{1}{2}$

D. $\sqrt{2}$
E. $\sqrt{3}$

Pembahasan Soal Nomor 30

Perhatikan gambar di atas
$\tan L= \dfrac{KM}{LM}$

$\cos L = \dfrac{LM}{KL}$

Untuk mencari nilai $\cos L$, pertama-tama kita harus mencari panjang sisi KL terlebih dahulu dengan menggunakan rumus phytagoras

$\begin{align} KL & = \sqrt{KM^{2} + LM^{2}}\\ & = \sqrt{\left (\sqrt {3}\right)^{2} + 3^{2}}\\ & = \sqrt{3+9}\\ & = \sqrt{12} \\ & = 2 \sqrt{3} \end{align}$

Maka nilai $\cos L$ adalah ......

$\begin{align} \cos L & = \dfrac{LM}{KL} \\ & = \dfrac{3}{2 \sqrt{3}}\\ & = \dfrac{3}{2 \sqrt{3}} \times \dfrac{\sqrt{3}}{\sqrt{3}} \\ & = \dfrac {1}{2} \sqrt{3} \end{align}$

Jadi, nilai $\cos L$ adalah $\dfrac {1}{2} \sqrt{3}$

Jawab : B

Demikianlah pembahasan soal UN Matematika SMA IPS 2017 part.6 No. 26 -30 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.

Lihat Juga :
Pembahasan Soal UN Matematika SMA IPS 2017 Part.7 No. 31 - 35

Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMA IPS No. 26 - 30". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.


Salam sukses untuk kita semua....!!!


Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini