Pembahasan Soal UN Matematika SMA IPS No. 31 - 35_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMA IPS tahun 2017 part 7. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Persamaan Trigonometri
- Aplikasi Trigonometri dalam kehidupan sehari-hari (soal cerita)
- Penafsiran Data Statistika
- Median Data Kelompok Statistika
- Varians Data Tunggal Statistika
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMA IPS 2017 Part.1 No. 1 - 5
2. Pembahasan Soal UN Matematika SMA IPS 2017 Part.2 No. 6 - 10
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.3 No. 11-15
3. Pembahasan Soal UN Matematika SMA IPS 2017 Part.4 No. 16-20
4. Pembahasan Soal UN Matematika SMA IPS 2017 Part.5 No. 21-25
5. Pembahasan Soal UN Matematika SMA IPS 2017 Part 6 No. 26-30
Soal Nomor 31
Himpunan penyelesaian dari persamaan $1 + 2 \sin x = 0,$ untuk $0^{\circ}\leq x \leq 360^{\circ}$ adalah .......A. $\left\{ 120^{\circ}, 180^{\circ}\right\}$
B. $\left\{ 150^{\circ}, 260^{\circ}\right\}$
C. $\left\{ 180^{\circ}, 270^{\circ}\right\}$
D. $\left\{ 200^{\circ}, 320^{\circ}\right\}$
E. $\left\{ 210^{\circ}, 330^{\circ}\right\}$
Pembahasan Soal Nomor 31
Penyelesaian :
Untuk menyelesaikan soal di atas, pertama-tama kita harus memindahkan bilangan yang tidak mengandung variabel x ke ruas sebelah kanan
$1 + 2 \sin x = 0 \\ 2 \sin x = 0-1 \\ 2 \sin x = -1 \\ \sin x = -\dfrac {1}{2}$
Untuk $\sin x$ yang bernilai negatif berada di Kuadran III dan IV
$\sin x = -\dfrac {1}{2}$
Kuadran III
$\sin x = sin \left (180^{\circ} + 30^{\circ} \right)\\ \begin {align} x & = 180^{\circ} + 30^{\circ} \\ & = 210^{\circ} \end {align}$
Kuadran IV
$\sin x = sin \left (360^{\circ} - 30^{\circ} \right)\\ \begin {align} x & = 360^{\circ} - 30^{\circ} \\ & = 330^{\circ} \end {align}$
Jadi, himpunan penyelesaian dari persamaan trigonometri di atas adalah $\left [210^{\circ},330^{\circ}\right]$
Jawab : E
Untuk menyelesaikan soal di atas, pertama-tama kita harus memindahkan bilangan yang tidak mengandung variabel x ke ruas sebelah kanan
$1 + 2 \sin x = 0 \\ 2 \sin x = 0-1 \\ 2 \sin x = -1 \\ \sin x = -\dfrac {1}{2}$
Untuk $\sin x$ yang bernilai negatif berada di Kuadran III dan IV
$\sin x = -\dfrac {1}{2}$
Kuadran III
$\sin x = sin \left (180^{\circ} + 30^{\circ} \right)\\ \begin {align} x & = 180^{\circ} + 30^{\circ} \\ & = 210^{\circ} \end {align}$
Kuadran IV
$\sin x = sin \left (360^{\circ} - 30^{\circ} \right)\\ \begin {align} x & = 360^{\circ} - 30^{\circ} \\ & = 330^{\circ} \end {align}$
Jadi, himpunan penyelesaian dari persamaan trigonometri di atas adalah $\left [210^{\circ},330^{\circ}\right]$
Jawab : E
Soal Nomor 32
Diketahui sudut elevansi pengamat terhadap puncak suatu menara televisi adalah $60^{\circ}$ dan jarak pengamat dari kaki menara 400 m. Tinggi menara tersebut adalah ........A. $800 $ m
B. $400\sqrt{3}$ m
C. $400\sqrt{2}$ m
D. $\dfrac{400}{3}\sqrt{2}$ m
E. $200$ m
Pembahasan Soal Nomor 32
Gambar Ilustrasi untuk soal Nomor 32
Untuk mencari tinggi menara dari soal di atas, kita dapat menggunakan konsep perbandingan trigonometri pada segitiga siku-siku.
Coba anda perhatikan gambar di atas!!!
Tinggi menara merupakan sisi segitiga yang berada di depan sudut. Sedangkan jarak kaki menara terhadap pengamat merupakan sisi segitiga di samping sudut.
Hubungan antara sisi depan sudut dengan sisi samping sudut pada segitiga mengingatkan kita dengan fungsi tangens dalam mencari besar sudut pada segitiga.
$\tan \alpha = \dfrac{\textbf{depan}}{\textbf{samping}}=\dfrac {\textbf{tinggi}}{\textbf{jarak}}$
Maka, tinggi menara tersebut adalah ....
$\tan \alpha = \dfrac {\textbf{depan}}{\textbf{samping}}=\dfrac {\textbf{tinggi}}{\textbf{jarak}}\\ \tan 60^{\circ} = \dfrac{t}{400}\\ \sqrt {3} = \dfrac{t}{400} \\ t = 400\sqrt {3}$
Jadi, tinggi menara tersebut adalah $400\sqrt {3}$
Jawab : B
Untuk mencari tinggi menara dari soal di atas, kita dapat menggunakan konsep perbandingan trigonometri pada segitiga siku-siku.
Coba anda perhatikan gambar di atas!!!
Tinggi menara merupakan sisi segitiga yang berada di depan sudut. Sedangkan jarak kaki menara terhadap pengamat merupakan sisi segitiga di samping sudut.
Hubungan antara sisi depan sudut dengan sisi samping sudut pada segitiga mengingatkan kita dengan fungsi tangens dalam mencari besar sudut pada segitiga.
$\tan \alpha = \dfrac{\textbf{depan}}{\textbf{samping}}=\dfrac {\textbf{tinggi}}{\textbf{jarak}}$
Maka, tinggi menara tersebut adalah ....
$\tan \alpha = \dfrac {\textbf{depan}}{\textbf{samping}}=\dfrac {\textbf{tinggi}}{\textbf{jarak}}\\ \tan 60^{\circ} = \dfrac{t}{400}\\ \sqrt {3} = \dfrac{t}{400} \\ t = 400\sqrt {3}$
Jadi, tinggi menara tersebut adalah $400\sqrt {3}$
Jawab : B
Soal Nomor 33
Tabel berikut adalah nilai hasil tes siswa yang di terima di kelas $X $ IPA.
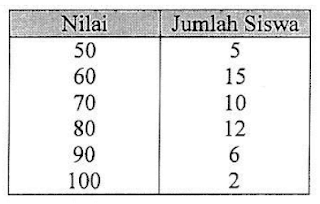
Siswa yang lulus dan dapat di terima adalah mereka yang mendapat nilai minimal 70. Persentase siswa yang tidak diterima adalah ......
A. 20%
B. 35%
C. 40%
D. 50%
E. 60%
Pembahasan Soal Nomor 33
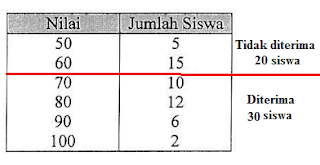
Gambar Ilustrasi Soal No. 33 (Tabel Nilai Siswa)
Berdasarkan data tabel di atas, dapat diketahui bahwa ada sebanyak 20 siswa yang tidak di terima dari total jumlah 50 siswa. Sehingga persentase yang tidak diterima adalah:
$\begin{align} \textbf{%} & = \dfrac {n}{\textbf{jumlah siswa}} \times 100\%\\ & = \dfrac {20}{50} x 100\% \\ & = 40 \% \end {align}$
Jadi, persentase siswa yang tidak diterima adalah $40 \%$
Jawab : C
Berdasarkan data tabel di atas, dapat diketahui bahwa ada sebanyak 20 siswa yang tidak di terima dari total jumlah 50 siswa. Sehingga persentase yang tidak diterima adalah:
$\begin{align} \textbf{%} & = \dfrac {n}{\textbf{jumlah siswa}} \times 100\%\\ & = \dfrac {20}{50} x 100\% \\ & = 40 \% \end {align}$
Jadi, persentase siswa yang tidak diterima adalah $40 \%$
Jawab : C
Soal Nomor 34
Nilai yang diperoleh peserta lomba matematika SMA tahun 2016 disajikan dalam histogram berikut.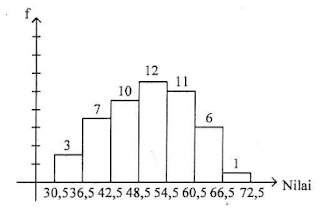
Median dari nilai lomba matematika tersebut adalah ........
A. 51,0
B. 51,5
C. 52,0
D. 52,5
E. 53,0
Pembahasan Soal Nomor 34
Rumus Median Data Berkelompok
Keterangan :
Me = Median
Tb = Tepi bawah kelas median
n = Jumlah seluruh frekuensi
F = Jumlah frekuensi sebelum kelas median
f = frekuensi kelas median
c = Panjang Kelas median
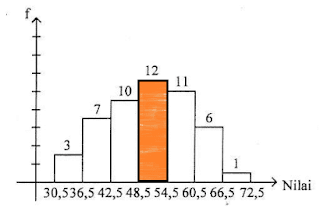
Perhatikan gambar di bawah ini :
Diketahui :
$ n = 50\\ Tb = 48,5\\ F = 20\\ f = 12\\ c = 6$
Maka, nilai mediannya adalah ....
$\begin {align} M_e & =T_b + \left [\dfrac{\dfrac{n}{2}- F}{f} \right ].c\\ & = 48,5 + \left [\dfrac{\dfrac{50}{2}- 20}{12} \right ].6 \\ & = 48,5 + \left [\dfrac {25- 20} {12} \right ].6 \\ & = 48,5 + \left [\dfrac {5} {12} \right ].6 \\ & = 48,5 + 2,5 \\ & = 51,0 \end {align}$
Jadi, nilai mediannya adalah $51,0$
Jawab : A
$M_e=T_b + \left [\dfrac{\dfrac{n}{2}- F}{f} \right ].c$
Keterangan :
Me = Median
Tb = Tepi bawah kelas median
n = Jumlah seluruh frekuensi
F = Jumlah frekuensi sebelum kelas median
f = frekuensi kelas median
c = Panjang Kelas median
Perhatikan gambar di bawah ini :
Diketahui :
$ n = 50\\ Tb = 48,5\\ F = 20\\ f = 12\\ c = 6$
Maka, nilai mediannya adalah ....
$\begin {align} M_e & =T_b + \left [\dfrac{\dfrac{n}{2}- F}{f} \right ].c\\ & = 48,5 + \left [\dfrac{\dfrac{50}{2}- 20}{12} \right ].6 \\ & = 48,5 + \left [\dfrac {25- 20} {12} \right ].6 \\ & = 48,5 + \left [\dfrac {5} {12} \right ].6 \\ & = 48,5 + 2,5 \\ & = 51,0 \end {align}$
Jadi, nilai mediannya adalah $51,0$
Jawab : A
Soal Nomor 35
Varian dari data 2, 5, 7, 6, 4, 5, 8, 3 adalah .......A. $0$
B. $\dfrac{12}{8}$
C.$\dfrac{14}{8}$
D.$\dfrac{18}{8}$
E.$\dfrac{28}{8}$
Pembahasan Soal Nomor 35
Rumus Varian Data Tunggal
Rumus Rata-rata Data Tunggal
Untuk mencari nilai varian dari data di atas, pertama-tama kita harus mencari nilai rata-ratanya terlebih dahulu
$\overline {x} = \dfrac {2+5+7+6+4+5+8+3}{8}\\ \overline {x} = \dfrac {40}{8}\\ \overline {x} = 5$
Agar lebih mudah dalam mencari nilai varians, sebaiknya kita membuat tabel bantuan seperti di bawah ini :
Tabel Bantuan Varian
Maka nilai variannya adalah ....
$\begin {align} \textbf{S}^{2} & = \dfrac {\displaystyle \sum_{i=1}^{n}{(x_i - \overline{x})^2}}{n} \\ & = \dfrac {28}{8} \end {align}$
Jadi, nilai variannya adalah $\dfrac {28}{8}$
Jawab : E
$\textbf{S}^{2}=\dfrac {\left (x_{1} - \overline {x}\right)^{2} + ...+\left (x_{n} - \overline {x}\right)^{2} }{n}$
atau
$\textbf{S}^{2} = \dfrac {\displaystyle \sum_{i=1}^{n}{(x_i - \overline{x})^2}}{n}$
dengan $\overline {x} =$ rata-rata dan $n =$ jumlah data
atau
$\textbf{S}^{2} = \dfrac {\displaystyle \sum_{i=1}^{n}{(x_i - \overline{x})^2}}{n}$
dengan $\overline {x} =$ rata-rata dan $n =$ jumlah data
Rumus Rata-rata Data Tunggal
$\overline {x} = \dfrac {x_1 + x_2 + ....+x_n}{n}$
Untuk mencari nilai varian dari data di atas, pertama-tama kita harus mencari nilai rata-ratanya terlebih dahulu
$\overline {x} = \dfrac {2+5+7+6+4+5+8+3}{8}\\ \overline {x} = \dfrac {40}{8}\\ \overline {x} = 5$
Agar lebih mudah dalam mencari nilai varians, sebaiknya kita membuat tabel bantuan seperti di bawah ini :
Tabel Bantuan Varian
$x$
|
$\overline {x}$
|
$x - \overline {x}$
|
$\left(x - \overline {x}\right)^{2}$
|
|---|---|---|---|
$2$
|
$5$
|
$-3$
|
$9$
|
$5$
|
$5$
|
$0$
|
$0$
|
$7$
|
$5$
|
$2$
|
$4$
|
$6$
|
$5$
|
$1$
|
$1$
|
$4$
|
$5$
|
$-1$
|
$1$
|
$5$
|
$5$
|
$0$
|
$0$
|
$8$
|
$5$
|
$3$
|
$9$
|
$3$
|
$5$
|
$-2$
|
$4$
|
Total
|
$28$
|
Maka nilai variannya adalah ....
$\begin {align} \textbf{S}^{2} & = \dfrac {\displaystyle \sum_{i=1}^{n}{(x_i - \overline{x})^2}}{n} \\ & = \dfrac {28}{8} \end {align}$
Jadi, nilai variannya adalah $\dfrac {28}{8}$
Jawab : E
Demikianlah pembahasan soal UN Matematika SMA IPS 2017 part.7 No. 31 -35 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
Lihat Juga :
Pembahasan Soal UN Matematika SMA IPS 2017 Part.8 No. 36 - 40
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMA IPS No. 31 - 35". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.


PERHATIAN !!!
Terima Kasih Telah Berkunjung ke Blog Caraono.com
1. Berkomentarlah dengan Baik dan Sopan
2. No Link Aktif
3. Mohon Maaf apabila ada pertanyaan anda yang belum atau tidak bisa dijawab karena saya manusia biasa bukan Google
Thanks for visiting and the comment :)
EmoticonEmoticon