
Pembahasan Soal UN Matematika SMP No. 6 - 10_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMP tahun 2017 part 2. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Aritmetika Sosial
- Perbandingan Bertingkat
- Skala
- Perbandingan Berbalik Nilai
- Relasi dan Fungsi (Pemetaan)
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMP 2017 Part.1 No. 1 - 5
Soal Nomor 6
Pak Andi menjual sepeda seharga $\textbf{Rp.}600.000,00$ dan mendapat keuntungan sebesar 20%. Harga beli sepeda tersebut adalah .........A. $\textbf{Rp.}420.000,00$
B. $\textbf{Rp.}450.000,00$
C. $\textbf{Rp.}500.000,00$
D. $\textbf{Rp.}720.000,00$
Pembahasan Soal Nomor 6
Penyelesaian
Dik
Harga Jual = Rp.600.000
Untung = 20% = 0,2
Harga beli = ?
Kita misalkan saja
Harga pembelian = x
Maka, harga pembeliannya adalah
Harga beli + Untung = Harga Jual
x + 0,2 = Rp.600.000
x (1 + 0,2) = Rp.600.000
1,2 x =Rp. 600.000
x = Rp.600.000 : 1,2
x = Rp. 500.000
Jadi, harga beli sepeda tersebut adalah Rp.500.000
Cara II
Rumus Mencari Harga Beli Jika Harga Jual dan Untungnya Diketahui
Rumus Mencari Harga Beli Jika Harga Jual dan Ruginya Diketahui
Maka, harga beli sepeda adalah
$\begin {align} \text{Harga Beli} & = \dfrac {100\%}{100\% + \% \text{untung}} \times \text {Harga Jual} \\ \\ & = \dfrac {100\%}{100\% + 20\%} \times \text {Rp. 600.000}\\ \\ & = \dfrac {100\%}{120\%} \times \text {Rp. 600.000}\\ \\ & = \dfrac {5}{6} \times \text {Rp. 600.000}\\ \\ & = \text {Rp. 500.000} \end {align}$
Jawab : C
Dik
Harga Jual = Rp.600.000
Untung = 20% = 0,2
Harga beli = ?
Kita misalkan saja
Harga pembelian = x
Maka, harga pembeliannya adalah
Harga beli + Untung = Harga Jual
x + 0,2 = Rp.600.000
x (1 + 0,2) = Rp.600.000
1,2 x =Rp. 600.000
x = Rp.600.000 : 1,2
x = Rp. 500.000
Jadi, harga beli sepeda tersebut adalah Rp.500.000
Cara II
Rumus Mencari Harga Beli Jika Harga Jual dan Untungnya Diketahui
$\begin {align}
\text{Harga Beli}
& = \dfrac {100\%}{100\% + \% \text{untung}} \times \text {Harga Jual} \\
\end {align}$
Rumus Mencari Harga Beli Jika Harga Jual dan Ruginya Diketahui
$\begin {align}
\text{Harga Beli}
& = \dfrac {100\%}{100\% - \% \text{rugi}} \times \text {Harga Jual} \\
\end {align}$
Maka, harga beli sepeda adalah
$\begin {align} \text{Harga Beli} & = \dfrac {100\%}{100\% + \% \text{untung}} \times \text {Harga Jual} \\ \\ & = \dfrac {100\%}{100\% + 20\%} \times \text {Rp. 600.000}\\ \\ & = \dfrac {100\%}{120\%} \times \text {Rp. 600.000}\\ \\ & = \dfrac {5}{6} \times \text {Rp. 600.000}\\ \\ & = \text {Rp. 500.000} \end {align}$
Jawab : C
Soal Nomor 7
Perbandingan umur Rahma, Fadhila, dan Taufik berturut-turut 8 : 3 : 10. Jika selisih umur Rahma dan Taufik adalah 4 tahun, maka jumlah umur mereka bertiga adalah.........A. 52 Tahun
B. 44 Tahun
C. 42 Tahun
D. 40 Tahun
Pembahasan Soal Nomor 7
Penyelesaian :
Dik :
Perbandingan umur Rahma, Fadhila, dan Taufik berturut-turut 8 : 3 : 10
selisih umur Rahma dan Taufik adalah 4 tahun
Misalkan :
Umur rahma = 8x
Umur Fadhila = 3x
Umur Taufik = 10x
Selisih umur Rahma dan Taufik adalah 4 tahun Maka,
$10x - 8x = 4 \\ \begin {align} 2x & = 4 \\ & = 2 \end {align}$
Sehingga Jumlah umur mereka bertiga adalah
$\begin {align}8x + 3x + 10x & = 21x \\ & = 21\left(2\right) \\ & = \text {42 Tahun} \end{align}$
Cara II
Jumlah Umur mereka adalah
$\begin {align} R + F + T & = \dfrac{8 + 3 + 10}{10 - 8} \times 4 \\ & = \dfrac{21}{2} \times 4 \\ & = \text {42 Tahun} \end {align}$
Jadi, Jumlah umur mereka bertiga adalah 42 Tahun
Jawab : C
Dik :
Perbandingan umur Rahma, Fadhila, dan Taufik berturut-turut 8 : 3 : 10
selisih umur Rahma dan Taufik adalah 4 tahun
Misalkan :
Umur rahma = 8x
Umur Fadhila = 3x
Umur Taufik = 10x
Selisih umur Rahma dan Taufik adalah 4 tahun Maka,
$10x - 8x = 4 \\ \begin {align} 2x & = 4 \\ & = 2 \end {align}$
Sehingga Jumlah umur mereka bertiga adalah
$\begin {align}8x + 3x + 10x & = 21x \\ & = 21\left(2\right) \\ & = \text {42 Tahun} \end{align}$
Cara II
Jumlah Umur mereka adalah
$\begin {align} R + F + T & = \dfrac{8 + 3 + 10}{10 - 8} \times 4 \\ & = \dfrac{21}{2} \times 4 \\ & = \text {42 Tahun} \end {align}$
Jadi, Jumlah umur mereka bertiga adalah 42 Tahun
Jawab : C
Soal Nomor 8
Seorang pemborong akan membangun kantor berukuran $70 \textbf{m} \times 90 \textbf{m}$. Pada denah terlihat ukuran kantor $14 \textbf{cm} \times 18 \textbf{cm}$. Skala denah tersebut adalah ..... A. $1 : 5.000$
B. $1 : 500$
C. $1 : 50$
D. $1 : 5$
Pembahasan Soal Nomor 8
Penyelesaian :
Skala adalah perbandingan ukuran pada gambar terhadap ukuran sebenarnya
Dik
Ukuran Sebenarnya = $70 \textbf{m} \times 90 \textbf{m}$
Ukuran pada Gambar (denah) =$14 \textbf{cm} \times 18 \textbf{cm}$
Untuk mencari Skala, pertama-tama kita harus menyamakan satuannya terlebih dahulu. Kita ubah satuan m = (meter) ke satuan cm (centimeter)
Mari kita ambil dan ubah salah satu satuannya saja, misalnya kita ambil satuan besaran panjang
panjang pada denah : 14 cm
panjang sebenarnya : 70 m = 7000 cm
Setelah, satuanya sama, mari kita cari skalanya
Maka, skala denah tersebut adalah
$\begin {align} \text {Skala} & = \text{JG} : \text{JS} \\ & = 14 : 7000 \\ & = 1 : 500 \end {align}$
Jadi, Skala pada denah tersebut adalah $1 : 500$
Jawab : B
Skala adalah perbandingan ukuran pada gambar terhadap ukuran sebenarnya
Dik
Ukuran Sebenarnya = $70 \textbf{m} \times 90 \textbf{m}$
Ukuran pada Gambar (denah) =$14 \textbf{cm} \times 18 \textbf{cm}$
Untuk mencari Skala, pertama-tama kita harus menyamakan satuannya terlebih dahulu. Kita ubah satuan m = (meter) ke satuan cm (centimeter)
Mari kita ambil dan ubah salah satu satuannya saja, misalnya kita ambil satuan besaran panjang
panjang pada denah : 14 cm
panjang sebenarnya : 70 m = 7000 cm
Setelah, satuanya sama, mari kita cari skalanya
$\textbf {Skala} = \text {JG} : \text {JS}$
Ket :
JG = Jarak (ukuran) pada gambar
JS = Jarak (ukuran) sebenarnya
Ket :
JG = Jarak (ukuran) pada gambar
JS = Jarak (ukuran) sebenarnya
Maka, skala denah tersebut adalah
$\begin {align} \text {Skala} & = \text{JG} : \text{JS} \\ & = 14 : 7000 \\ & = 1 : 500 \end {align}$
Jadi, Skala pada denah tersebut adalah $1 : 500$
Jawab : B
Soal Nomor 9
Burhan dapat menyelesaikan pekerjaan mencangkul sebidang lahan pertanian dalam waktu 4 hari dan Khoidir dapat menyelesaikan dalam waktu 12 hari. Jika mereka bekerja bersama-sama, maka waktu yang dibutuhkan adalah ........A. 2 hari
B. 3 hari
C. 4 hari
D. 6 hari
Pembahasan Soal Nomor 9
Logikanya, Jika suatu pekerjaan dikerjakan bersama-sama, maka yang bertambah di sini adalah kecepatan mereka bekerja atau waktu yang dibutuhkan semakin singkat.
Penyelesaian :
Burhan = 4 Hari
Burhan x 4 hari = 1 lahan, maka
$\text {1 hari} = \dfrac {1}{4} \text {lahan}$
Khoidir = 12 Hari
Khoidir x 12 hari = 1 lahan, maka
$\text {1 hari} = \dfrac {1}{12} \text {lahan}$
Ditanya :
Burhan + Khoidir = x hari
Ketika mereka bekerja bersama sampai selesai selama n hari.
$ bn + kn = 1 \\ n (b + k) = 1 \\ n = \dfrac {1}{b + k}\\ n = \dfrac {1}{\dfrac {1}{4} + \dfrac {1}{12} } \\ n = \dfrac {1}{\dfrac {3 + 1}{12}} \\ n = \dfrac {1}{\dfrac {4}{12}} \\ \begin {align} n & = 1 : \dfrac {4}{12} \\ & = 1 \times \dfrac {12}{4} \\ & = \text {3 hari} \end {align}$
Cara Kedua (II)
Menggunakan Rumus
$t_x$ adalah waktu yang dibutuhkan dalam mengerjakan pekerjaan secara bersama.
$t_A$ adalah waktu yang dibutuhkan si A dalam menyelesaikan pekerjaan dan
$t_B$ adalah waktu yang dibutuhkan si B dalam menyelesaikan pekerjaan
Jika mereka bekerja bersama-sama, maka waktu yang dibutuhkan adalah
$\dfrac {1}{t_{x}} = \dfrac {1}{t_{A}} + \dfrac {1}{t_{B}}\\ \dfrac {1}{t_{x}} = \dfrac {1}{4} + \dfrac {1}{12}\\ \dfrac {1}{t_{x}} = \dfrac {3 + 1}{12} \\ \dfrac {1}{t_{x}} = \dfrac {4}{12} \\ t_x = \dfrac {12}{4} \\ t_x = \text {3 hari}$
Cara Tiga
$\begin {align} \text{B} + \text{K} & = \dfrac {\left (\text{B} \times \text{K}\right)}{\left (\text{B} + \text{K}\right)} \\ & = \dfrac {\left (4 \times 12\right)}{\left (4 +12 \right)} \\ & = \dfrac {48}{16}\\ & = \text {3 hari} \end {align}$
Jadi, waktu yang dibutuhkan jika Burhan dan Khoidir bekerja sama adalah 3 hari
Jawab : B
Penyelesaian :
Burhan = 4 Hari
Burhan x 4 hari = 1 lahan, maka
$\text {1 hari} = \dfrac {1}{4} \text {lahan}$
Khoidir = 12 Hari
Khoidir x 12 hari = 1 lahan, maka
$\text {1 hari} = \dfrac {1}{12} \text {lahan}$
Ditanya :
Burhan + Khoidir = x hari
Ketika mereka bekerja bersama sampai selesai selama n hari.
$ bn + kn = 1 \\ n (b + k) = 1 \\ n = \dfrac {1}{b + k}\\ n = \dfrac {1}{\dfrac {1}{4} + \dfrac {1}{12} } \\ n = \dfrac {1}{\dfrac {3 + 1}{12}} \\ n = \dfrac {1}{\dfrac {4}{12}} \\ \begin {align} n & = 1 : \dfrac {4}{12} \\ & = 1 \times \dfrac {12}{4} \\ & = \text {3 hari} \end {align}$
Cara Kedua (II)
Menggunakan Rumus
$\dfrac {1}{t_{x}} = \dfrac {1}{t_{A}} + \dfrac {1}{t_{B}}$
Keterangan $t_x$ adalah waktu yang dibutuhkan dalam mengerjakan pekerjaan secara bersama.
$t_A$ adalah waktu yang dibutuhkan si A dalam menyelesaikan pekerjaan dan
$t_B$ adalah waktu yang dibutuhkan si B dalam menyelesaikan pekerjaan
Jika mereka bekerja bersama-sama, maka waktu yang dibutuhkan adalah
$\dfrac {1}{t_{x}} = \dfrac {1}{t_{A}} + \dfrac {1}{t_{B}}\\ \dfrac {1}{t_{x}} = \dfrac {1}{4} + \dfrac {1}{12}\\ \dfrac {1}{t_{x}} = \dfrac {3 + 1}{12} \\ \dfrac {1}{t_{x}} = \dfrac {4}{12} \\ t_x = \dfrac {12}{4} \\ t_x = \text {3 hari}$
Cara Tiga
$\begin {align} \text{B} + \text{K} & = \dfrac {\left (\text{B} \times \text{K}\right)}{\left (\text{B} + \text{K}\right)} \\ & = \dfrac {\left (4 \times 12\right)}{\left (4 +12 \right)} \\ & = \dfrac {48}{16}\\ & = \text {3 hari} \end {align}$
Jadi, waktu yang dibutuhkan jika Burhan dan Khoidir bekerja sama adalah 3 hari
Jawab : B
Soal Nomor 10
Perhatikan diagram panah disamping ! 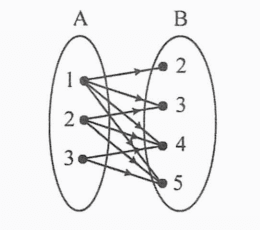
Relasi dari himpunan A ke himpunan B adalah ........
A. Satu kurangnnya dari
B. Kurang dari
C. Faktor dari
D. Lebih dari
Pembahasan Soal Nomor 10
Perhatikan Gambar di atas
Anggota himpunan A adalah {1, 2, 3 } dan
Anggota himpunan B adalah {2, 3, 4, 5 }
Setelah itu, perhatikan Setiap pasangan Anggota Himpunan A
Anggota himpunan A berpasangan dengan Anggota Himpunan B
#Pertama.
Angka 1 pada himpunan A berpasangan dengan angka 2, 3, 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"1 kurang dari 2, 3, 4, atau 5"
# Kedua.
Angka 2 pada himpunan A berpasangan dengan angka 3, 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"2 kurang dari 3, 4, atau 5"
#Ketiga.
Angka 3 pada himpunan A berpasangan dengan angka 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"3 kurang dari 4, atau 5"
Jadi, relasi dari himpunan A ke himpunan B adalah ‘kurang dari’
Jawab : B
Anggota himpunan A adalah {1, 2, 3 } dan
Anggota himpunan B adalah {2, 3, 4, 5 }
Setelah itu, perhatikan Setiap pasangan Anggota Himpunan A
Anggota himpunan A berpasangan dengan Anggota Himpunan B
#Pertama.
Angka 1 pada himpunan A berpasangan dengan angka 2, 3, 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"1 kurang dari 2, 3, 4, atau 5"
# Kedua.
Angka 2 pada himpunan A berpasangan dengan angka 3, 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"2 kurang dari 3, 4, atau 5"
#Ketiga.
Angka 3 pada himpunan A berpasangan dengan angka 4, 5 pada himpunan B, Hal ini berarti hubungan yang di peroleh adalah
"3 kurang dari 4, atau 5"
Jadi, relasi dari himpunan A ke himpunan B adalah ‘kurang dari’
Jawab : B
Demikianlah pembahasan soal UN Matematika SMP 2017 part.2 No. 6 -10 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
Lihat Juga :
Pembahasan Soal UN Matematika SMP 2017 No. 11 - 15
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMP No. 6 - 10". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.
PERHATIAN !!!
Terima Kasih Telah Berkunjung ke Blog Caraono.com
1. Berkomentarlah dengan Baik dan Sopan
2. No Link Aktif
3. Mohon Maaf apabila ada pertanyaan anda yang belum atau tidak bisa dijawab karena saya manusia biasa bukan Google
Thanks for visiting and the comment :)
EmoticonEmoticon