Pembahasan Soal UN Matematika SMP 2017 No. 11 - 15

Pembahasan Soal UN Matematika SMP No. 11 - 15_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMP tahun 2017 part 3. Pada edisi kali ini soal-soalnya berisikan materi tentang :

1. Persamaan Linier Satu Variabel
2. Persamaan Garis Lurus
3. Himpunan
4. SPLDV & Bagun Datar
5. Operasi Bentuk Aljabar

Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMP 2017 Part.1 No. 1 - 5
2. Pembahasan Soal UN Matematika SMP 2017 Part.2 No. 6 - 10

Soal Nomor 11

Jika $k$ merupakan penyelesaian dari $5 \left(7x - 4 \right) = -3 \left(-9x + 12 \right) + 8$, nilai $k-7$ adalah .........
A. $-8$
B. $-6$
C. $-5$
D. $-2$

Pembahasan Soal Nomor 11

Penyelesaian :
Untuk menyelesaikan soal di atas, kita harus menyederhanakannya hingga di dapat nilai x nya
$\begin {align} 5 \left(7x - 4 \right) & = -3 \left(-9x + 12 \right) + 8 \\ 35x - 20 & = 27x - 36 + 8 \\ 35x - 27x & = - 36 + 8 + 20\\ 8x & = -8 \\ x & = -1 \end {align}$

Nilai $x = -1$ adalah nilai $k$, maka nilai $k-7$ adalah
$\begin {align} k-7 & = - 1 - 7 \\ & = -8 \end {align}$

Jadi, nilai $k-7$ adalah $-8$

Jawab : A

Soal Nomor 12

Persamaan garis yang melalui titik $\left ( -2,3 \right)$ dan bergradien $-3$ adalah .........
A. $x + 3y + 3 = 0$
B. $x - 3y + 3 = 0$
C. $3x + y + 3 = 0$
D. $3x - y + 3 = 0$

Pembahasan Soal Nomor 12

Penyelesaian :
Persamaan garis melalui titik $\left (x_{1}, y_{1}\right)$ dan bergradien $m$ dirumuskan sebagai
$ \bbox[yellow,5px,border:2px solid red] { y - y_1 = m\left (x - x_1\right) \qquad (1) } $

Dik :
$\left ( x_1,y_1 \right) =\left ( -2,3 \right) \\ m = - 3$


Maka, persamaan garisnya adalah
$\begin {align} y - y_1 & = m\left (x - x_1\right) \\ y - 3 & = -3 \left (x + 2 \right) \\ y - 3 & = -3x -6 \\ y - 3 + 3x + 6 & = 0 \\ y + 3x + 3 & = 0 \\ 3x + y + 3 & = 0 \end {align}$

Jadi, persamaan garisnya adalah $3x + y + 3 = 0$


Jawab : C

Soal Nomor 13

Diketahui himpunan B = {bilangan prima kurang dari 15}. Banyak himpunan bagian dari B yang mempunyai 3 anggota adalah ........
A. $6$
B. $15$
C. $16$
D. $20$

Pembahasan Soal Nomor 13

Penyelesaian :
Himpunan B adalah bilangan prima kurang dari 15, maka
$B = \{2, 3, 5, 7, 11, 13 \}$
$n\left (B\right) = 6$

Banyak himpunan bagian dari B yang beranggotakan 3 dapat dicari melalui segitiga pascal berikut ini.


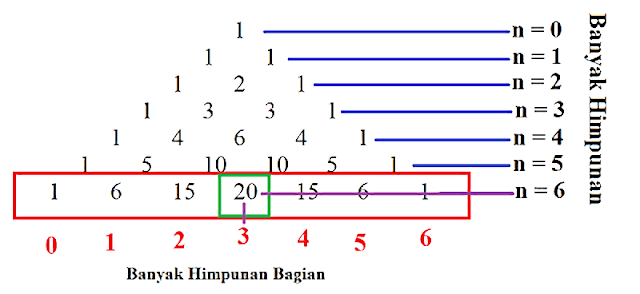
Maksud dari masing-masing bilangan adalah.

1. Banyaknya himpunan bagian yang memiliki 0 anggota yaitu ada 1.
2. Banyaknya himpunan bagian yang memiliki 1 anggota yaitu ada 6.
3. Banyaknya himpunan bagian yang memiliki 2 anggota yaitu ada 15.
4. Banyaknya himpunan bagian yang memiliki 3 anggota yaitu ada 20.
5. Banyaknya himpunan bagian yang memiliki 4 anggota yaitu ada 15.
6. Banyaknya himpunan bagian yang memiliki 5 anggota yaitu ada 6.
7. Banyaknya himpunan bagian yang memiliki 6 anggota yaitu ada 1.

Jadi, banyak himpunan bagian dari B yang mempunyai 3 anggota adalah 20


Cara Manual (Mengurutkannya satu-persatu)
{(2,3,5); (2,3,7); (2,3,11); (2,3,13); (2,5,7); (2,5,11); (2,5,13); (2,7,11); (2,7,13); (2,11,13); (3,5,7); (3,5,11); (3,5,13); (3,7,11); (3,7,13); (3,11,13); (5,7,11); (5,7,13); (5,11,13); (7,11,13)}


Jadi, banyak himpunan bagian dari B yang mempunyai 3 anggota adalah 20

Jawab : D

Soal Nomor 14

Keliling persegi panjang 80 cm. Jika selisih panjang dan lebarnya 12 cm, luasnya adalah ........
A. $480cm^{2}$
B. $420cm^{2}$
C. $364cm^{2}$
D. $288cm^{2}$

Pembahasan Soal Nomor 14

Penyelesaian :
Diketahui
Selisih panjang dan lebarnya 12 cm
$\begin {align} p-l & = 12 \\ p & =12 + l ..........\text {pers.1} \end {align}$

Keliling persegi panjang 80 cm, maka
$\begin {align} K & = 80 \\ 2\left(p + l\right) & = 80\\ p + l & = 40 ...........\text{pers. 2} \end {align}$

Setelah itu, kita subtitusikan pers. 1 ke per 2
$\begin {align} p + l & = 40\\ \left ( 12 + l\right) + l & = 40 \\ 12 + 2l & = 40 \\ 2l & = 40 - 12 \\ 2l & = 28 \\ l & = 14 cm \end {align}$

Setelah itu, kita cari panjangnya dengan mensubtitusikan nilai $l = 14$ ke pers, 2
$\begin {align} p + l & = 40\\ p + \left (14 \right) & = 40 \\ p & = 40 - 14 \\ p & = 26 cm \end {align}$

Maka Luas persegi panjang adalah
$\begin {align} L & = p \times l\\ & = 26 \times 14 \\ & = 364 cm^{2} \end {align}$

Jadi, Luas persegi panjang adalah $364 cm^{2}$


Jawab : C

Soal Nomor 15

Bentuk sederhana dari $5x^{2} - 2xy - 8y^{2} - 6x^{2} - xy + 3y^{2}$ adalah ........
A. $-x^{2} - 3xy + 5y^{2}$
B. $-x^{2} - 3xy - 5y^{2}$
C. $x^{2} + 3xy + 5y^{2}$
D. $x^{2} + 3xy + 5y^{2}$

Pembahasan Soal Nomor 15

Penyelesaian :
Untuk menyelesaikan soal di atas, pertama-tama kita harus mengelompokkannya dengan suku-suku yang sejenis. lalu setelah itu, baru kita operasikan seperti biasanya.

$5x^{2} - 2xy - 8y^{2} - 6x^{2} - xy + 3y^{2}\\ = 5x^{2} - 6x^{2} - 2xy - xy - 8y^{2} + 3y^{2}\\ = -x^{2} - 3xy -5y^{2}$

Jadi, bentuk sederhana dari $5x^{2} - 2xy - 8y^{2} - 6x^{2} - xy + 3y^{2}$ adalah $-x^{2} - 3xy -5y^{2}$


Jawab : B

Demikianlah pembahasan soal UN Matematika SMP  2017 part.3 No. 11 -15 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.

Lihat Juga :
Pembahasan Soal UN Matematika SMP 2017 No. 16 - 20

Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMP  No. 11 - 15". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.


Salam sukses untuk kita semua....!!!


Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.