
Pembahasan Soal UN Matematika SMP No. 16 - 20_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMP tahun 2017 part 4. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Fungsi
- Bangun Datar
- Sistem Persamaan Linier Dua Variabel (SPLDV)
- Diagram Venn
- Lingkaran_Bangun Datar
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMP 2017 Part.1 No. 1 - 5
2. Pembahasan Soal UN Matematika SMP 2017 Part.2 No. 6 - 10
3. Pembahasan Soal UN Matematika SMP 2017 Part.3 No. 11-15
Soal Nomor 16
Fungsi $f$ dirumuskan dengan $f\left(x\right)= 15 - 2x .$ Jika $f\left(b\right)=7,$ nilai $b$ adalah .........A. $-4$
B. $1$
C. $4$
D. $11$
Pembahasan Soal Nomor 16
Penyelesaian :
Untuk menentukan nilai $b$ pada $f\left(b\right) =7$, kita harus berpatokkan pada $f\left(x\right)=15 -2x$ dengan mensubtitusikan $x = b$
$\begin {align} f\left(x\right) & = 15 - 2x \\ f\left(b\right) & = 15 - 2b \\ 7 & = 15 - 2b \\ 2b & = 15 - 7\\ 2b & = 8 \\ b & = 4 \end {align}$
Jadi, nilai $b$ adalah $4$
Jawab : C
Untuk menentukan nilai $b$ pada $f\left(b\right) =7$, kita harus berpatokkan pada $f\left(x\right)=15 -2x$ dengan mensubtitusikan $x = b$
$\begin {align} f\left(x\right) & = 15 - 2x \\ f\left(b\right) & = 15 - 2b \\ 7 & = 15 - 2b \\ 2b & = 15 - 7\\ 2b & = 8 \\ b & = 4 \end {align}$
Jadi, nilai $b$ adalah $4$
Jawab : C
Soal Nomor 17
Taman bunga Pak Rahman membentuk persegipanjang dengan ukuran panjang diagonalnya $\left(3x + 15\right)$ meter dan $\left(5x + 5\right)$ meter. Panjang diagonal taman bunga tersebut adalah .........A. 10 meter
B. 25 meter
C. 30 meter
D. 55 meter
Pembahasan Soal Nomor 17
Penyelesaian :
Diketahui :
$d_{1} = \left(3x + 15\right) \\ d_{2} = \left(5x + 5\right)$
Karena panjang diagonal pada persegipanjang adalah sama maka $d_{1} =d_{2} $
$\begin {align} d_{1} & = d_{2} \\ 3x + 15 & = 5x + 5 \\ 15 - 5 & = 5x -3x \\ 10 & = 2x \\ x & = 5 \end {align}$
Setelah itu, nilai $x = 5$ kita subtitusikan ke salah satu persamaan diagonal, misalnya kita pilih $d_{1}$ saja.
$\begin {align} d_{1} & = 3x + 15 \\ & = 3\left(5\right) + 15 \\ & = 15 + 5 \\ & = \text {30 meter} \end {align}$
Jadi, panjang diagonal taman bunga tersebut adalah $\text {30 meter}$
Jawab : C
Diketahui :
$d_{1} = \left(3x + 15\right) \\ d_{2} = \left(5x + 5\right)$
Karena panjang diagonal pada persegipanjang adalah sama maka $d_{1} =d_{2} $
$\begin {align} d_{1} & = d_{2} \\ 3x + 15 & = 5x + 5 \\ 15 - 5 & = 5x -3x \\ 10 & = 2x \\ x & = 5 \end {align}$
Setelah itu, nilai $x = 5$ kita subtitusikan ke salah satu persamaan diagonal, misalnya kita pilih $d_{1}$ saja.
$\begin {align} d_{1} & = 3x + 15 \\ & = 3\left(5\right) + 15 \\ & = 15 + 5 \\ & = \text {30 meter} \end {align}$
Jadi, panjang diagonal taman bunga tersebut adalah $\text {30 meter}$
Jawab : C
Soal Nomor 18
Diketahui $x - 3y - 5 = 0$ dan $2x - 5y= 9.$ Nilai dari $3x + 2y$ adalah .......A. $-1$
B. $1$
C. $3$
D. $4$
Pembahasan Soal Nomor 18
Penyelesaian :
Untuk menyelesaikan soal di atas, pertama-tama kita harus mencari nilai $x$ dan $y$ dari persamaan di bawah ini.
$x - 3y - 5 = 0 ...\Rightarrow x = 3y + 5 .....\text{pers. 1}\\ 2x - 5y= 9 ..........\text{pers. 2}$
# Mencari nilai $x$ dan $y$
Pertama, Kita subtitusikan persamaan 1 ke persamaan 2
$\begin {align} 2x - 5y & = 9 \\ 2\left(3y + 5\right) -5y & = 9 \\ 6y + 10 - 5y & = 9 \\ y + 10 & = 9 \\ y & = 9 - 10 \\ y & = -1 \end {align}$
Kedua, Setelah itu nilai $y = -1$ kita subtitusikan lagi kepersamaan di atas, misal kita pilih pers. 1
$\begin {align} x & = 3y + 5 \\ & = 3\left(-1\right) + 5 \\ & = -3 + 5 \\ & = 2 \end {align}$
Ketiga, setelah itu nilai $x$ dan $y$ nya diketahui, maka kita tinggal mensubtitusikan ke persamaan $3x + 2y.$ Maka nilai dari $3x + 2y$ adalah
$\begin {align} 3x + 2y & = 3\left(2\right) + 2\left(-1\right)\\ & = 6 - 2 \\ & = 4 \end {align}$
Jadi nilai dari $3x + 2y$ adalah $4$
Jawab : D
Untuk menyelesaikan soal di atas, pertama-tama kita harus mencari nilai $x$ dan $y$ dari persamaan di bawah ini.
$x - 3y - 5 = 0 ...\Rightarrow x = 3y + 5 .....\text{pers. 1}\\ 2x - 5y= 9 ..........\text{pers. 2}$
# Mencari nilai $x$ dan $y$
Pertama, Kita subtitusikan persamaan 1 ke persamaan 2
$\begin {align} 2x - 5y & = 9 \\ 2\left(3y + 5\right) -5y & = 9 \\ 6y + 10 - 5y & = 9 \\ y + 10 & = 9 \\ y & = 9 - 10 \\ y & = -1 \end {align}$
Kedua, Setelah itu nilai $y = -1$ kita subtitusikan lagi kepersamaan di atas, misal kita pilih pers. 1
$\begin {align} x & = 3y + 5 \\ & = 3\left(-1\right) + 5 \\ & = -3 + 5 \\ & = 2 \end {align}$
Ketiga, setelah itu nilai $x$ dan $y$ nya diketahui, maka kita tinggal mensubtitusikan ke persamaan $3x + 2y.$ Maka nilai dari $3x + 2y$ adalah
$\begin {align} 3x + 2y & = 3\left(2\right) + 2\left(-1\right)\\ & = 6 - 2 \\ & = 4 \end {align}$
Jadi nilai dari $3x + 2y$ adalah $4$
Jawab : D
Soal Nomor 19
Suatu regu pramuka beranggotakan 25 orang. 12 orang membawa tongkat, 15 orang membawa bendera semapur, dan 6 orang tidak membawa keduanya. Jumlah anggota yang membawa kedua alat itu adalah ........A. 2 orang
B. 8 orang
C. 21 orang
D. 27 orang
Pembahasan Soal Nomor 19
Penyelesaian :
Data pada soal di atas dapat disajikan dalam bentuk diagram Venn
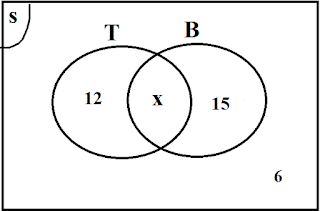
Keterangan
T = Orang yang membawa tongkat
B = Orang yang membawa Bendera semapur
X = Orang yang membawa keduanya (Tongkat dan Bendera semapur)
Ditanyakan
Nilai x atau orang yang membawa kedua alat itu ?
Maka Jumlah anggota yang membawa alat itu adalah
Banyak orang yang membawa tongkat saja + Banyak orang yang membawa bendera semapur saja + Banyak orang yang membawa tongkat dan bendera semapur + Banyak orang yang tidak membawa tongkat dan bendera semapur = 25
$\begin {align} \left(12 - x\right) + \left(15 - x\right) + x + 6 & = 25 \\ 33 - x & = 25 \\ 33 - 25 & = x \\ x & = 8 \end {align}$
Jadi, Jumlah orang yang membawa kedua alat itu ada $\text {8 orang}$
Jawab : B
Data pada soal di atas dapat disajikan dalam bentuk diagram Venn

Keterangan
T = Orang yang membawa tongkat
B = Orang yang membawa Bendera semapur
X = Orang yang membawa keduanya (Tongkat dan Bendera semapur)
Ditanyakan
Nilai x atau orang yang membawa kedua alat itu ?
Maka Jumlah anggota yang membawa alat itu adalah
Banyak orang yang membawa tongkat saja + Banyak orang yang membawa bendera semapur saja + Banyak orang yang membawa tongkat dan bendera semapur + Banyak orang yang tidak membawa tongkat dan bendera semapur = 25
$\begin {align} \left(12 - x\right) + \left(15 - x\right) + x + 6 & = 25 \\ 33 - x & = 25 \\ 33 - 25 & = x \\ x & = 8 \end {align}$
Jadi, Jumlah orang yang membawa kedua alat itu ada $\text {8 orang}$
Jawab : B
Soal Nomor 20
Keliling sebuah lingkaran adalah $\text {31,4 cm}.$ Luas lingkaran tersebut adalah ........$\left(\pi=3,14\right)$A. $\text {78,5 cm}^{2}$
B. $\text {62,8 cm}^{2}$
C. $\text {314 cm}^{2}$
D. $\text {628 cm}^{2}$
Pembahasan Soal Nomor 20
Penyelesaian :
Dik ;
$\text {K} = \text {31,4 cm} \\ \pi=3,14$
Ditanya :
Luas lingkaran = ?
Cara I
Mencari Nilai r terlebih dahulu
$\begin {align} K & = 31,4 \\ 2.\pi.r & = 31,4 \\ 2 \times 3,14 \times r & = 31,4 \\ 6,28 r & = 31,4 \\ r & = 5 \end {align}$
Maka luas lingkarannya adalah
$\begin {align} \textbf {L} & = \pi.r^{2} \\ & = 3,14 \times 5^{2} \\ & = 3,14 \times 25 \\ & = 78,5 \end {align}$
Cara II
Menggunakan Rumus Hubungan Antara Keliling dan Luas Lingkaran
$\begin {align} \textbf{L} & = \dfrac {\text {K}^{2}}{4.\pi} \\ & = \dfrac {31,4^{2}}{4 \times 3,14} \\ & = \dfrac {985,96}{12,56} \\ & = 78,5 \end {align}$
Jadi, luas lingkaran adalah $\text {78,5 cm}^{2}$
Jawab : A
Dik ;
$\text {K} = \text {31,4 cm} \\ \pi=3,14$
Ditanya :
Luas lingkaran = ?
Cara I
Mencari Nilai r terlebih dahulu
$\begin {align} K & = 31,4 \\ 2.\pi.r & = 31,4 \\ 2 \times 3,14 \times r & = 31,4 \\ 6,28 r & = 31,4 \\ r & = 5 \end {align}$
Maka luas lingkarannya adalah
$\begin {align} \textbf {L} & = \pi.r^{2} \\ & = 3,14 \times 5^{2} \\ & = 3,14 \times 25 \\ & = 78,5 \end {align}$
Cara II
Menggunakan Rumus Hubungan Antara Keliling dan Luas Lingkaran
$\begin {align} \textbf{L} & = \dfrac {\text {K}^{2}}{4.\pi} \\ & = \dfrac {31,4^{2}}{4 \times 3,14} \\ & = \dfrac {985,96}{12,56} \\ & = 78,5 \end {align}$
Jadi, luas lingkaran adalah $\text {78,5 cm}^{2}$
Jawab : A
Demikianlah pembahasan soal UN Matematika SMP 2017 part.4 No. 16 -20 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
Lihat Juga :
Pembahasan Soal UN Matematika SMP 2017 No. 21 - 25
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMP No. 16 - 20". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.
PERHATIAN !!!
Terima Kasih Telah Berkunjung ke Blog Caraono.com
1. Berkomentarlah dengan Baik dan Sopan
2. No Link Aktif
3. Mohon Maaf apabila ada pertanyaan anda yang belum atau tidak bisa dijawab karena saya manusia biasa bukan Google
Thanks for visiting and the comment :)
EmoticonEmoticon