
Pembahasan Soal UN Matematika SMA IPS No. 6 - 10_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas soal UN Matematika SMA IPS tahun 2017 part 2. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Fungsi Kuadrat
- Akar Persamaan Kuadrat
- Persamaan Kuadrat Baru
- Penerapan Fungsi Kuadrat
- Sistem Persamaan Linier
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan sebelumnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMA IPS 2017 Part.1 No. 1 - 5
Soal Nomor 6
Perhatikan gambar!
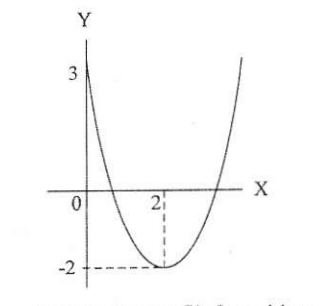
Persaman grafix fungsi kuadrat dari gambar tersebut adalah .......
A. $y=\dfrac{4}{5}x^{2}-4x + 3$
B. $y=\dfrac{5}{4}x^{2}-5x + 3$
C. $y=\dfrac{4}{5}x^{2}+4x - 3$
D. $y=\dfrac{5}{4}x^{2}-5x - 3$
F. $y=\dfrac{5}{4}x^{2}+5x + 3$

Persaman grafix fungsi kuadrat dari gambar tersebut adalah .......
A. $y=\dfrac{4}{5}x^{2}-4x + 3$
B. $y=\dfrac{5}{4}x^{2}-5x + 3$
C. $y=\dfrac{4}{5}x^{2}+4x - 3$
D. $y=\dfrac{5}{4}x^{2}-5x - 3$
F. $y=\dfrac{5}{4}x^{2}+5x + 3$
Pembahasan Soal Nomor 6
Rumus-rumus yang digunakan :
Grafik fungsi kuadrat yang mempunyai titik puncak atau titik balik P $\left (x_{p}, y_{p}\right)$ dan melalui sebuah titik tertentu.
Persamaan fungsi kuadrat tersebut dapat dinyatakan sebagai berikut :
Analisa soal
Grafik fungsi kuadrat pada gambar di atas mempunyai puncak (2,-2) dan melalui titik (0.3)
Selanjutnya kita subtitusikan titik puncak $\left (x_{p}=2 ,y_{p}=-2\right) $ ke rumus di atas :
$y= a \left (x - x_{p}\right)^{2} + y_{p}$
$y= a \left (x - 2\right)^{2} + \left (-2\right)$
$y= a \left (x - 2\right)^{2} -2$........Pers.1
Selanjutnya, kita mencari nilai a dengan mensubtitusikan titik $\left (0,3\right)$ ke pers. 1
$y= a \left (x - 2\right)^{2} -2$
$3= a \left (0 - 2\right)^{2} -2$
$3= 4a -2$
$5 = 4a$
$a = \dfrac {5}{4}$
Selanjutnya, kita akan mencari persamaan grafik fungsi kuadrat dengan mensubtitusikan nilai $a$ ke pers. 1
$y= a \left (x - 2\right)^{2} -2$
$y= \dfrac {5}{4}\left (x - 2\right)^{2} -2$
$y= \dfrac {5}{4}\left (x^{2} -4x + 4\right) -2$
$y= \dfrac {5}{4}x^{2}- 5x + 5 - 2$
$y= \dfrac {5}{4}x^{2}- 5x + 3 $
Jawab : B
Grafik fungsi kuadrat yang mempunyai titik puncak atau titik balik P $\left (x_{p}, y_{p}\right)$ dan melalui sebuah titik tertentu.
Persamaan fungsi kuadrat tersebut dapat dinyatakan sebagai berikut :
$y=f\left (x\right )= a \left (x - x_{p}\right)^{2} + y_{p}$
Dengan nilai a ditentukan kemudian.
Analisa soal
Grafik fungsi kuadrat pada gambar di atas mempunyai puncak (2,-2) dan melalui titik (0.3)
Selanjutnya kita subtitusikan titik puncak $\left (x_{p}=2 ,y_{p}=-2\right) $ ke rumus di atas :
$y= a \left (x - x_{p}\right)^{2} + y_{p}$
$y= a \left (x - 2\right)^{2} + \left (-2\right)$
$y= a \left (x - 2\right)^{2} -2$........Pers.1
Selanjutnya, kita mencari nilai a dengan mensubtitusikan titik $\left (0,3\right)$ ke pers. 1
$y= a \left (x - 2\right)^{2} -2$
$3= a \left (0 - 2\right)^{2} -2$
$3= 4a -2$
$5 = 4a$
$a = \dfrac {5}{4}$
Selanjutnya, kita akan mencari persamaan grafik fungsi kuadrat dengan mensubtitusikan nilai $a$ ke pers. 1
$y= a \left (x - 2\right)^{2} -2$
$y= \dfrac {5}{4}\left (x - 2\right)^{2} -2$
$y= \dfrac {5}{4}\left (x^{2} -4x + 4\right) -2$
$y= \dfrac {5}{4}x^{2}- 5x + 5 - 2$
$y= \dfrac {5}{4}x^{2}- 5x + 3 $
Jawab : B
Soal Nomor 7
Misalkan $x_{1}$ dan $x_{2}$ adalah akar-akar persamaan kuadrat $x^{2}+3x-28=0$. Jika $x_{1} < x_{2},$ maka nilai $3x_{1}+2x_{2}$ adalah ......A. $-13$
B. $-3$
C. $-2$
D. $2$
E. $13$
Pembahasan Soal Nomor 7
Rumus-rumus yang digunakan :
Untuk mencari akar-akar dari persamaan kuadrat, ada 3 cara yang bisa dilakukan yaitu (1), Dengan cara memfaktorkan, (2) Melengkapkan bentuk kuadrat dan (3) Menggunakan Rumus ABC.
Namun sayang, pada kesempatan kali ini saya hanya akan menggunakan salah satunya saja yaitu dengan cara memfaktorkan.
$x^{2}+3x-28=0$
$\left (x + 7\right)\left (x -4\right)=0$
$x=-7$ atau $x=4$
Karena $x_{1} < x_{2},$ maka :
$x_{1}=-7, x_{2}=4$
Selanjutnya, subtitusikan nilai $x_{1}$ dan $x_{2}$
$3x_{1}+2x_{2} $
$= 3\left (-7\right)+ 2\left (4\right)$
$ = -21 + 8 $
$= - 13$
Jawab : A
Untuk mencari akar-akar dari persamaan kuadrat, ada 3 cara yang bisa dilakukan yaitu (1), Dengan cara memfaktorkan, (2) Melengkapkan bentuk kuadrat dan (3) Menggunakan Rumus ABC.
Namun sayang, pada kesempatan kali ini saya hanya akan menggunakan salah satunya saja yaitu dengan cara memfaktorkan.
$x^{2}+3x-28=0$
$\left (x + 7\right)\left (x -4\right)=0$
$x=-7$ atau $x=4$
Karena $x_{1} < x_{2},$ maka :
$x_{1}=-7, x_{2}=4$
Selanjutnya, subtitusikan nilai $x_{1}$ dan $x_{2}$
$3x_{1}+2x_{2} $
$= 3\left (-7\right)+ 2\left (4\right)$
$ = -21 + 8 $
$= - 13$
Jawab : A
Soal Nomor 8
Misalkan $x_{1}$ dan $x_{2}$ adalah akar-akar persamaan kuadrat $2x^{2}+6x+7=0$. Persamaan kuadrat yang akar-akarnya $\left ( 2x_{1}+1 \right )$
dan $\left ( 2x_{2}+1 \right )$ adalah ........A. $x^{2}-8x+9=0$
B. $x^{2}-8x+14=0$
C. $x^{2}-8x+21=0$
D. $x^{2}-4x+9=0$
E. $x^{2}-4x+21=0$
Pembahasan Soal Nomor 8
Rumus-rumus yang digunakan :
Untuk menyusun persamaan kuadrat baru kita dapat menggunakan rumus jumlah dan hasil kali akar-akar persamaan kuadrat.
Secara umum, rumus persamaan kuadrat baru adalah sebagai berikut :
Langkah-langah menyusun persamaan kuadrat baru
1. Tentukan jumlah akar persamaan kuadrat lama (awal)
2 Tentukan hasil kali akar persamaan kuadrat lama
3. Tentukan jumlah akar persamaan kuadrat baru
4. Tentukan hasil kali akar persamaan kuadrat baru
5. Susun persamaan kuadrat baru
Dari persamaan kuadrat lama $2x^{2}+6x+7=0$ diketahui :
a = 2, b= -6, dan c = 7
1. Jumlah akar persamaan kuadrat lama
$x_{1} + x_{2} = -\dfrac {b}{a}=\dfrac {6}{2}=3$ ........(1)
2. Hasil kali akar persamaan kuadrat lama
$x_{1} \times x_{2}= \dfrac {c}{a} = \dfrac {7}{2}$ .......(2)
Selanjutnya, kita tentukan jumlah akar dan hasil kali akar dari akar-akar persamaan kuadrat baru.
3. Jumlah akar persamaan kuadrat baru
$x_{1} + x_{2} = \left ( 2x_{1}+1 \right ) + \left ( 2x_{2}+1 \right )$
$x_{1} + x_{2} = 2x_{1} + 2x_{2} + 2 $
$x_{1} + x_{2} = 2 \left (x_{1} + x_{2}\right) + 2$
$x_{1} + x_{2} = 2\left(3\right) + 2$ ......subt. pers. 1
$x_{1} + x_{2} = 8$
4. Hasil kali akar persamaan kuadrat baru
$x_{1} \times x_{2}= \left ( 2x_{1}+1 \right )\times\left ( 2x_{2}+1 \right )$
$x_{1} \times x_{2}= 4x_{1}x_{2} + 2x_{1} + 2x_{2}+ 1$
$x_{1} \times x_{2}= 4 \left ( x_{1}x_{1} \right ) + 2\left ( x_{1}+ x_{1}\right ) +1$
$x_{1} \times x_{2}= 4 \left ( \dfrac {7}{2}\right ) + 2\left ( 3\right ) + 1 $ ......subt. pers. 1 & 2
$x_{1} \times x_{2}= 14 + 6 + 1$
$x_{1} \times x_{2}= 21$
5. Menyusun persamaan kuadrat baru dengan menggunakan rumus di atas.
Maka, persamaan kuadrat barunya adalah :
${x}^{2} - $ Jumlah akar $x +$ hasil kali akar $= 0$
$x^{2} - 8x + 21 = 0$
Jawab : C
Untuk menyusun persamaan kuadrat baru kita dapat menggunakan rumus jumlah dan hasil kali akar-akar persamaan kuadrat.
Secara umum, rumus persamaan kuadrat baru adalah sebagai berikut :
${x}^{2} - $ Jumlah akar $x +$ hasil kali akar $= 0$
atau
$\mathbf{x^{2} - \left ( \alpha +\beta \right)x + \alpha\beta=0} $
Dengan $\alpha$ dan $\beta$ adalah akar-akar dari persamaan kuadrat baru. Langkah-langah menyusun persamaan kuadrat baru
1. Tentukan jumlah akar persamaan kuadrat lama (awal)
2 Tentukan hasil kali akar persamaan kuadrat lama
3. Tentukan jumlah akar persamaan kuadrat baru
4. Tentukan hasil kali akar persamaan kuadrat baru
5. Susun persamaan kuadrat baru
Dari persamaan kuadrat lama $2x^{2}+6x+7=0$ diketahui :
a = 2, b= -6, dan c = 7
1. Jumlah akar persamaan kuadrat lama
$x_{1} + x_{2} = -\dfrac {b}{a}=\dfrac {6}{2}=3$ ........(1)
2. Hasil kali akar persamaan kuadrat lama
$x_{1} \times x_{2}= \dfrac {c}{a} = \dfrac {7}{2}$ .......(2)
Selanjutnya, kita tentukan jumlah akar dan hasil kali akar dari akar-akar persamaan kuadrat baru.
3. Jumlah akar persamaan kuadrat baru
$x_{1} + x_{2} = \left ( 2x_{1}+1 \right ) + \left ( 2x_{2}+1 \right )$
$x_{1} + x_{2} = 2x_{1} + 2x_{2} + 2 $
$x_{1} + x_{2} = 2 \left (x_{1} + x_{2}\right) + 2$
$x_{1} + x_{2} = 2\left(3\right) + 2$ ......subt. pers. 1
$x_{1} + x_{2} = 8$
4. Hasil kali akar persamaan kuadrat baru
$x_{1} \times x_{2}= \left ( 2x_{1}+1 \right )\times\left ( 2x_{2}+1 \right )$
$x_{1} \times x_{2}= 4x_{1}x_{2} + 2x_{1} + 2x_{2}+ 1$
$x_{1} \times x_{2}= 4 \left ( x_{1}x_{1} \right ) + 2\left ( x_{1}+ x_{1}\right ) +1$
$x_{1} \times x_{2}= 4 \left ( \dfrac {7}{2}\right ) + 2\left ( 3\right ) + 1 $ ......subt. pers. 1 & 2
$x_{1} \times x_{2}= 14 + 6 + 1$
$x_{1} \times x_{2}= 21$
5. Menyusun persamaan kuadrat baru dengan menggunakan rumus di atas.
Maka, persamaan kuadrat barunya adalah :
${x}^{2} - $ Jumlah akar $x +$ hasil kali akar $= 0$
$x^{2} - 8x + 21 = 0$
Jawab : C
Soal Nomor 9
Total penjualan suatu barang $\left ( k\right )$ merupakan perkalian antara harga $\left ( p\right )$ dan permintaan $\left ( x\right )$ dinyatakan dengan $k = px$. Untuk $p=90-3x$ dalam jutaan rupiah dan $1\leq x\leq 30$, maka total penjualan maksimum adalah .........A. Rp. 1.350.000.000,00
B. Rp. 675.000.000,00
C. Rp. 600.000.000,00
D. Rp. 450.000.000,00
E. Rp. 45.000.000,00
Pembahasan Soal Nomor 9
Diketahui :
$k =px $
$p= 90 - 3x $
$1\leq x\leq 30$
Selanjutnya, membuat model matematika dari persoalan di atas.
pertama, subtitusikan nilai $p$ ke $k =px $ hingga di peroleh fungsi kuadrat $k$ sebagai berikut :
$k =px $
$ k = \left (90-3x\right)x$
$k = 90x - 3x^{2}$
$k =- 3x^{2} + 90x$
Selanjutnya, kita mencari nilai $x$ agar fungsi $k$ maksimum. Nah, Untuk mencari nilai $x$, ada dua cara yang bisa kita gunakan pertama, menggunakan rumus sumbu simetri fungsi kuadrat dan kedua, menggunakan turunan (diferensial).
#1. Rumus sumbu simetri fungsi kuadrat
berdasarkan fungsi kuadrat $k =- 3x^{2} + 90x$ di peroleh :
$a = -3, b = 90 , c = 0 $
Rumus sumbu simetri
$x = -\dfrac {b}{2a}$
$x = -\dfrac {90}{2\left (-3\right)}$
$x = \dfrac {90}{6}$
$x = 15$
#2. Menggunakan turunan
$k^{'}=0$
$-6x + 90=0$
$90= 6x$
$x = 15$
Selanjutya nilai $x$ tersebut kita subtitusikan ke fungsi $k$
$k\left (x\right) = -3x^{2} + 90x$
$k\left (15\right) = -3\left(15\right)^{2} + 90\left(15\right)$
$k\left (15\right) = -675 + 1350 $
$k\left (15\right) = 675$ (dalam jutaan rupiah )
Jadi, total penjualan maksimum barang $k$ adalah $Rp.675.000.000,-$
Jawab : B
$k =px $
$p= 90 - 3x $
$1\leq x\leq 30$
Selanjutnya, membuat model matematika dari persoalan di atas.
pertama, subtitusikan nilai $p$ ke $k =px $ hingga di peroleh fungsi kuadrat $k$ sebagai berikut :
$k =px $
$ k = \left (90-3x\right)x$
$k = 90x - 3x^{2}$
$k =- 3x^{2} + 90x$
Selanjutnya, kita mencari nilai $x$ agar fungsi $k$ maksimum. Nah, Untuk mencari nilai $x$, ada dua cara yang bisa kita gunakan pertama, menggunakan rumus sumbu simetri fungsi kuadrat dan kedua, menggunakan turunan (diferensial).
#1. Rumus sumbu simetri fungsi kuadrat
berdasarkan fungsi kuadrat $k =- 3x^{2} + 90x$ di peroleh :
$a = -3, b = 90 , c = 0 $
Rumus sumbu simetri
$x = -\dfrac {b}{2a}$
$x = -\dfrac {b}{2a}$
$x = -\dfrac {90}{2\left (-3\right)}$
$x = \dfrac {90}{6}$
$x = 15$
#2. Menggunakan turunan
$k^{'}=0$
$-6x + 90=0$
$90= 6x$
$x = 15$
Selanjutya nilai $x$ tersebut kita subtitusikan ke fungsi $k$
$k\left (x\right) = -3x^{2} + 90x$
$k\left (15\right) = -3\left(15\right)^{2} + 90\left(15\right)$
$k\left (15\right) = -675 + 1350 $
$k\left (15\right) = 675$ (dalam jutaan rupiah )
Jadi, total penjualan maksimum barang $k$ adalah $Rp.675.000.000,-$
Jawab : B
Soal Nomor 10
Misalkan $\left ( a,b\right )=\left ( a_{1},b_{1}\right )$ adalah penyelesaian dari sistem persamaan $\left\{\begin{matrix}
2a-7b=-16 & \\
a+8b=15&
\end{matrix}\right.,$ maka nilai $a_{1}+2b_{1}$ adalah ........A. $-3$
B. $-1$
C. $0$
D. $1$
E. $3$
Pembahasan Soal Nomor 10
Rumus-rumus yang digunakan :
Cara Untuk menyelesaikan Sistem persamaan Linear yang paling umum dan banyak digunakan adalah Metode Subtitusi, Metode Eleminasi dan Metode Kombinasi Eliminasi-Subtitusi.
Dan Pada kesempatan ini, saya akan menggunakan metode kombinasi Eliminasi-Subtitusi untuk menyelesaikan SPL di atas.
$ \left.\begin{matrix} 2a - 7b = -16 \\ a + 8b = 15 \end{matrix}\right| \left.\begin{matrix} \times 1\\ \times 2 \end{matrix}\right| \begin{matrix} 2a - 7b = -16 \\ 2a + 16b = 30 \end{matrix} \begin{matrix} & \\ & \left ( - \right ) \end{matrix} $
-----------------------------------------------------------
$-23b = -46$
$b = 2 $
Selanjutnya nilai b = 2 kita subtitusikan ke salah satu persamaan linier di atas misalnya saya pilih pers. yang kedua.
$a + 8b= 15$
$a + 8\left (2\right) = 15$
$a + 16= 15$
$a = 15 - 16$
$a = -1$
Sehingga diperoleh,
$a_{1} = -1$
$b_{1} = 2$
Maka nilai dari $a_{1}+2b_{1}$ adalah.....
$a_{1}+2b_{1}$
$= -1 +2\left (2\right)$
$=-1+4 $
$= 3$
Jawab : E
Cara Untuk menyelesaikan Sistem persamaan Linear yang paling umum dan banyak digunakan adalah Metode Subtitusi, Metode Eleminasi dan Metode Kombinasi Eliminasi-Subtitusi.
Dan Pada kesempatan ini, saya akan menggunakan metode kombinasi Eliminasi-Subtitusi untuk menyelesaikan SPL di atas.
$ \left.\begin{matrix} 2a - 7b = -16 \\ a + 8b = 15 \end{matrix}\right| \left.\begin{matrix} \times 1\\ \times 2 \end{matrix}\right| \begin{matrix} 2a - 7b = -16 \\ 2a + 16b = 30 \end{matrix} \begin{matrix} & \\ & \left ( - \right ) \end{matrix} $
-----------------------------------------------------------
$-23b = -46$
$b = 2 $
Selanjutnya nilai b = 2 kita subtitusikan ke salah satu persamaan linier di atas misalnya saya pilih pers. yang kedua.
$a + 8b= 15$
$a + 8\left (2\right) = 15$
$a + 16= 15$
$a = 15 - 16$
$a = -1$
Sehingga diperoleh,
$a_{1} = -1$
$b_{1} = 2$
Maka nilai dari $a_{1}+2b_{1}$ adalah.....
$a_{1}+2b_{1}$
$= -1 +2\left (2\right)$
$=-1+4 $
$= 3$
Jawab : E
Demikianlah pembahasan soal UN Matematika SMA IPS 2017 part.2 No. 6 - 10 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
Pembahasan Soal UN Matematika SMA IPS 2017 Part.3 No. 11 - 15
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMA IPS No. 6 - 10". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
PERHATIAN !!!
Terima Kasih Telah Berkunjung ke Blog Caraono.com
1. Berkomentarlah dengan Baik dan Sopan
2. No Link Aktif
3. Mohon Maaf apabila ada pertanyaan anda yang belum atau tidak bisa dijawab karena saya manusia biasa bukan Google
Thanks for visiting and the comment :)
EmoticonEmoticon